Gegenbauer Differential Equation
المؤلف:
Abramowitz, M. and Stegun, I. A
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
12-6-2018
2190
Gegenbauer Differential Equation
The second-order ordinary differential equation
 |
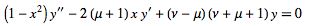(1)
|
sometimes called the hyperspherical differential equation (Iyanaga and Kawada 1980, p. 1480; Zwillinger 1997, p. 123). The solution to this equation is
![y=(x^2-1)^(-mu/2)[C_1P_nu^mu(x)+C_2Q_nu^mu(x)],](http://mathworld.wolfram.com/images/equations/GegenbauerDifferentialEquation/NumberedEquation2.gif) |
(2)
|
where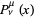 
is an associated Legendre function of the first kind and 
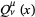is an associated Legendre function of the second kind.
A number of other forms of this equation are sometimes also known as the ultraspherical or Gegenbauer differential equation, including
 |
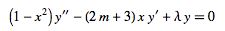(3)
|
The general solutions to this equation are
![y=(x^2-1)^((1-2mu)/4)[C_1P_(-1/2+mu+nu)^(1/2-mu)(x)+C_2Q_(-1/2+mu+nu)^(1/2-mu)(x)].](http://mathworld.wolfram.com/images/equations/GegenbauerDifferentialEquation/NumberedEquation4.gif) |
(4)
|
If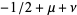 
is an integer, then one of the solutions is known as a Gegenbauer polynomials 
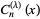, also known as ultraspherical polynomials.
The form
 |
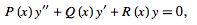(5)
|
is also given by Infeld and Hull (1951, pp. 21-68) and Zwillinger (1997, p. 122). It has the solution
![y=(x^2-1)^(-(2m+1)/4)[C_1P_(-1/2+sqrt((1+m)^2+lambda))^(1/2+m)(x)+C_2Q_(-1/2+sqrt((1+m)^2+lambda))^(1/2+m)(x)].](http://mathworld.wolfram.com/images/equations/GegenbauerDifferentialEquation/NumberedEquation6.gif) |
(6)
|
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.
Infeld, L. and Hull, T. E. "The Factorization Method." Rev. Mod. Phys. 23, 21-68, 1951.
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, 1980.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 547-549, 1953.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 127, 1997.
الاكثر قراءة في معادلات تفاضلية
اخر الاخبار
اخبار العتبة العباسية المقدسة
