Dirichlet Problem
المؤلف:
Courant, R. and Hilbert, D
المصدر:
Methods of Mathematical Physics, Vol. 1. New York: Wiley
الجزء والصفحة:
...
26-12-2018
1664
Dirichlet Problem
The problem of finding the connection between a continuous function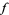 
on the boundary 
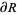of a region 
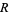with a harmonic function taking on the value 
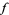on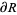 
. In general, the problem asks if such a solution exists and, if so, if it is unique. The Dirichlet problem is extremely important in mathematical physics (Courant and Hilbert 1989, pp. 179-180 and 240; Logan 1997; Krantz 1999b).
If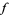 
is a continuous function on the boundary of the open unit disk 
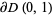, then define
![u(z)=<span style=]() {1/(2pi)int_0^(2pi)f(e^(ipsi))(1-|z|^2)/(|z-e^(ipsi)|^2)dpsi if z in D(0,1); f(z) if z in partialD(0,1), " src="http://mathworld.wolfram.com/images/equations/DirichletProblem/NumberedEquation1.gif" style="height:74px; width:325px" /> |
(1)
|
where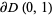 
is the boundary of 
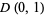. Then 
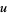is continuous on the closed unit disk 
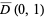and harmonic on 
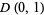(Krantz 1999a, p. 93).
For the case of rational boundary data without poles, the resulting solution of the Dirichlet problem is also rational (Ebenfelt and Viscardi 2005), the proof of which led to Viscardi winning the 2005-2006 Siemens-Westinghouse competition (Siemens Foundation 2005; Mathematical Association of America 2006).
REFERENCES:
Courant, R. and Hilbert, D. Methods of Mathematical Physics, Vol. 1. New York: Wiley, pp. 179-180 and 240, 1989.
Ebenfelt, P. and Viscardi, M. "On the Solution of the Dirichlet Problem with Rational Holomorphic Boundary Data." Comput. Meth. Func. Th. 5, 445-457, 2005. http://www.heldermann.de/CMF/CMF05/CMF052/cmf05027.htm.
Krantz, S. G. "The Dirichlet Problem" and "Application of Conformal Mapping to the Dirichlet Problem." §7.3.3, 7.7.1, and 14.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 93, 97-98, and 164-168, 1999a.
Krantz, S. G. A Panorama of Harmonic Analysis. Washington, DC: Math. Assoc. Amer., 1999b.
Logan, J. D. Applied Mathematics, 2nd ed. New York: Wiley, 1997.
Mathematical Association of America. "Mathematics Student Wins the Siemens-Westinghouse Competition." Jan. 9, 2006. http://www.maa.org/news/010906westinghouse.html.
Siemens Foundation. "2005 Siemens Competition Nationals." http://www.siemens-foundation.org/competition/2005/2005Nationals.htm#Michael.
الاكثر قراءة في معادلات تفاضلية
اخر الاخبار
اخبار العتبة العباسية المقدسة
