Harmonic Function
المؤلف:
Ash, J. M. (Ed.)
المصدر:
Studies in Harmonic Analysis. Washington, DC: Math. Assoc. Amer., 1976.
الجزء والصفحة:
...
26-12-2018
1252
Harmonic Function
Any real function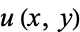 
with continuous second partial derivatives which satisfies Laplace's equation,
 |
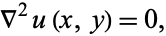(1)
|
is called a harmonic function. Harmonic functions are called potential functions in physics and engineering. Potential functions are extremely useful, for example, in electromagnetism, where they reduce the study of a 3-component vector field to a 1-component scalar function. A scalar harmonic function is called a scalar potential, and a vector harmonic function is called a vector potential.
To find a class of such functions in the plane, write the Laplace's equation in polar coordinates
 |
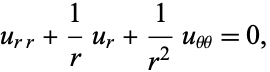(2)
|
and consider only radial solutions
 |
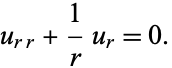(3)
|
This is integrable by quadrature, so define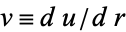 
,
 |
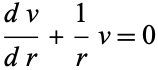(4)
|
 |
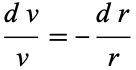(5)
|
 |
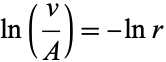(6)
|
 |
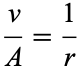(7)
|
 |
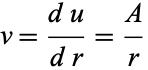(8)
|
 |
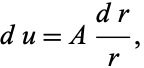(9)
|
so the solution is
 |
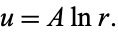(10)
|
Ignoring the trivial additive and multiplicative constants, the general pure radial solution then becomes
Other solutions may be obtained by differentiation, such as
and
 |
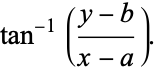(17)
|
Harmonic functions containing azimuthal dependence include
The Poisson kernel
 |
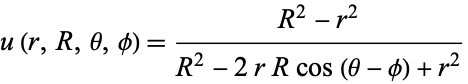(20)
|
is another harmonic function.
REFERENCES:
Ash, J. M. (Ed.). Studies in Harmonic Analysis. Washington, DC: Math. Assoc. Amer., 1976.
Axler, S.; Bourdon, P.; and Ramey, W. Harmonic Function Theory. Springer-Verlag, 1992.
Benedetto, J. J. Harmonic Analysis and Applications. Boca Raton, FL: CRC Press, 1996.
Cohn, H. Conformal Mapping on Riemann Surfaces. New York: Dover, 1980.
Krantz, S. G. "Harmonic Functions." §1.4.1 and Ch. 7 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 16 and 89-101, 1999.
Weisstein, E. W. "Books about Potential Theory." http://www.ericweisstein.com/encyclopedias/books/PotentialTheory.html.
الاكثر قراءة في معادلات تفاضلية
اخر الاخبار
اخبار العتبة العباسية المقدسة
