

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Double Factorial
المؤلف:
Arfken, G
المصدر:
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press
الجزء والصفحة:
...
15-5-2019
4107
The double factorial of a positive integer 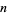 is a generalization of the usual factorial
is a generalization of the usual factorial 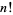 defined by
defined by
|
(1) |
Note that 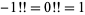 , by definition (Arfken 1985, p. 547).
, by definition (Arfken 1985, p. 547).
The origin of the notation 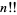 appears not to not be widely known and is not mentioned in Cajori (1993).
appears not to not be widely known and is not mentioned in Cajori (1993).
For 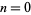 , 1, 2, ..., the first few values are 1, 1, 2, 3, 8, 15, 48, 105, 384, ... (OEIS A006882). The numbers of decimal digits in
, 1, 2, ..., the first few values are 1, 1, 2, 3, 8, 15, 48, 105, 384, ... (OEIS A006882). The numbers of decimal digits in 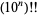 for
for 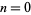 , 1, ... are 1, 4, 80, 1285, 17831, 228289, 2782857, 32828532, ... (OEIS A114488).
, 1, ... are 1, 4, 80, 1285, 17831, 228289, 2782857, 32828532, ... (OEIS A114488).
The double factorial is implemented in the Wolfram Language as n!! or Factorial2[n].
The double factorial is a special case of the multifactorial.
The double factorial can be expressed in terms of the gamma function by
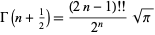 |
(2) |
(Arfken 1985, p. 548).
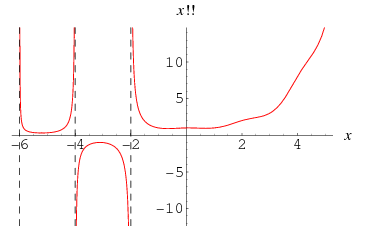
The double factorial can also be extended to negative odd integers using the definition
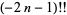 |
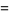 |
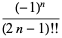 |
(3) |
 |
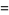 |
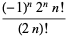 |
(4) |
for 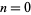 , 1, ... (Arfken 1985, p. 547).
, 1, ... (Arfken 1985, p. 547).
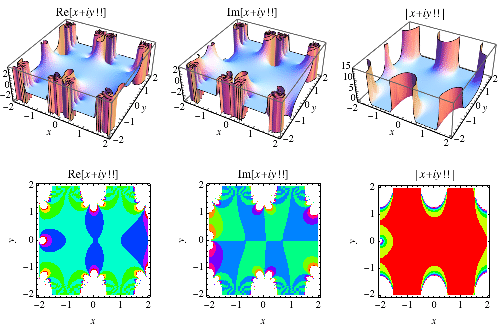 |
Similarly, the double factorial can be extended to complex arguments as
![z!!=2^([1+2z-cos(piz)]/4)pi^([cos(piz)-1]/4)Gamma(1+1/2z).](http://mathworld.wolfram.com/images/equations/DoubleFactorial/NumberedEquation3.gif) |
(5) |
There are many identities relating double factorials to factorials. Since
![(2n+1)!!2^nn!
=[(2n+1)(2n-1)...1][2n][2(n-1)][2(n-2)]...2·1
=[(2n+1)(2n-1)...1][2n(2n-2)(2n-4)...2]
=(2n+1)(2n)(2n-1)(2n-2)(2n-3)(2n-4)...2·1
=(2n+1)!,](http://mathworld.wolfram.com/images/equations/DoubleFactorial/NumberedEquation4.gif) |
(6) |
it follows that 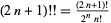 . For
. For 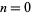 , 1, ..., the first few values are 1, 3, 15, 105, 945, 10395, ... (OEIS A001147).
, 1, ..., the first few values are 1, 3, 15, 105, 945, 10395, ... (OEIS A001147).
Also, since
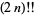 |
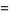 |
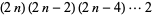 |
(7) |
 |
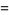 |
![[2(n)][2(n-1)][2(n-2)]...2](http://mathworld.wolfram.com/images/equations/DoubleFactorial/Inline22.gif) |
(8) |
 |
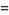 |
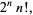 |
(9) |
it follows that 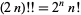 . For
. For 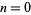 , 1, ..., the first few values are 1, 2, 8, 48, 384, 3840, 46080, ... (OEIS A000165).
, 1, ..., the first few values are 1, 2, 8, 48, 384, 3840, 46080, ... (OEIS A000165).
Finally, since
![(2n-1)!!2^nn!
=[(2n-1)(2n-3)...1][2n][2(n-1)][2(n-2)]...2(1)
=(2n-1)(2n-3)...1][2n(2n-2)(2n-4)...2]
=2n(2n-1)(2n-2)(2n-3)(2n-4)...2(1)
=(2n)!,](http://mathworld.wolfram.com/images/equations/DoubleFactorial/NumberedEquation5.gif) |
(10) |
it follows that
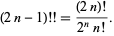 |
(11) |
For 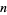 odd,
odd,
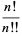 |
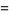 |
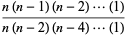 |
(12) |
 |
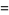 |
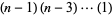 |
(13) |
 |
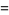 |
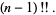 |
(14) |
For 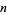 even,
even,
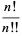 |
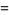 |
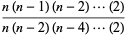 |
(15) |
 |
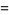 |
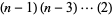 |
(16) |
 |
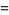 |
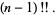 |
(17) |
Therefore, for any 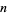 ,
,
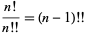 |
(18) |
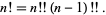 |
(19) |
The double factorial satisfies the beautiful series
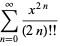 |
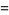 |
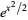 |
(20) |
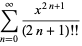 |
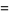 |
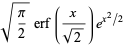 |
(21) |
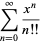 |
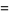 |
![1/2e^(x^2/2)[sqrt(2pi)erf(x/(sqrt(2)))+2].](http://mathworld.wolfram.com/images/equations/DoubleFactorial/Inline57.gif) |
(22) |
The latter gives rhe sum of reciprocal double factorials in closed form as
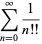 |
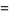 |
![sqrt(e)[1+sqrt(pi/2)erf(1/2sqrt(2))]](http://mathworld.wolfram.com/images/equations/DoubleFactorial/Inline60.gif) |
(23) |
 |
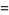 |
![sqrt(e)[1/2sqrt(2)+gamma(1/2,1/2)]](http://mathworld.wolfram.com/images/equations/DoubleFactorial/Inline63.gif) |
(24) |
 |
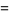 |
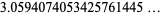 |
(25) |
(OEIS A143280), where 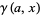 is a lower incomplete gamma function. This sum is a special case of the reciprocal multifactorial constant.
is a lower incomplete gamma function. This sum is a special case of the reciprocal multifactorial constant.
A closed-form sum due to Ramanujan is given by
![sum_(n=0)^infty(-1)^n[((2n-1)!!)/((2n)!!)]^3=[(Gamma(9/8))/(Gamma(5/4)Gamma(7/8))]^2](http://mathworld.wolfram.com/images/equations/DoubleFactorial/NumberedEquation9.gif) |
(26) |
(Hardy 1999, p. 106). Whipple (1926) gives a generalization of this sum (Hardy 1999, pp. 111-112).
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 544-545 and 547-548, 1985.
Cajori, F. A History of Mathematical Notations, Vol. 2. New York: Dover, 1993.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Meserve, B. E. "Double Factorials." Amer. Math. Monthly 55, 425-426, 1948.
Sloane, N. J. A. Sequences A000165/M1878, A001147/M3002, A006882/M0876, A114488, and A143280 in "The On-Line Encyclopedia of Integer Sequences."
Whipple, F. J. W. "On Well-Poised Series, Generalised Hypergeometric Series Having Parameters in Pairs, Each Pair with the Same Sum." Proc. London Math. Soc. 24, 247-263, 1926.