

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Spherical Harmonic
المؤلف:
Abbott, P
المصدر:
"2. Schrödinger Equation." Lecture Notes for Computational Physics 2. http://physics.uwa.edu.au/pub/Computational/CP2/2.Schroedinger.nb.
الجزء والصفحة:
...
6-8-2019
3334
The spherical harmonics 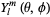 are the angular portion of the solution to Laplace's equation in spherical coordinates where azimuthal symmetry is not present. Some care must be taken in identifying the notational convention being used. In this entry,
are the angular portion of the solution to Laplace's equation in spherical coordinates where azimuthal symmetry is not present. Some care must be taken in identifying the notational convention being used. In this entry, 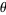 is taken as the polar (colatitudinal) coordinate with
is taken as the polar (colatitudinal) coordinate with ![theta in [0,pi]](http://mathworld.wolfram.com/images/equations/SphericalHarmonic/Inline3.gif) , and
, and 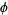 as the azimuthal (longitudinal) coordinate with
as the azimuthal (longitudinal) coordinate with 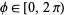 . This is the convention normally used in physics, as described by Arfken (1985) and the Wolfram Language (in mathematical literature,
. This is the convention normally used in physics, as described by Arfken (1985) and the Wolfram Language (in mathematical literature, 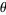 usually denotes the longitudinal coordinate and
usually denotes the longitudinal coordinate and 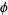 the colatitudinal coordinate). Spherical harmonics are implemented in the Wolfram Language as SphericalHarmonicY[l, m, theta, phi].
the colatitudinal coordinate). Spherical harmonics are implemented in the Wolfram Language as SphericalHarmonicY[l, m, theta, phi].
Spherical harmonics satisfy the spherical harmonic differential equation, which is given by the angular part of Laplace's equation in spherical coordinates. Writing 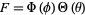 in this equation gives
in this equation gives
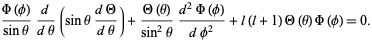 |
(1)
|
Multiplying by 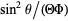 gives
gives
![[(sintheta)/(Theta(theta))d/(dtheta)(sintheta(dTheta)/(dtheta))+l(l+1)sin^2theta]+1/(Phi(phi))(d^2Phi(phi))/(dphi^2)=0.](http://mathworld.wolfram.com/images/equations/SphericalHarmonic/NumberedEquation2.gif) |
(2)
|
Using separation of variables by equating the 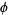 -dependent portion to a constant gives
-dependent portion to a constant gives
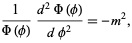 |
(3)
|
which has solutions
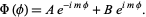 |
(4)
|
Plugging in (3) into (2) gives the equation for the 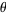 -dependent portion, whose solution is
-dependent portion, whose solution is
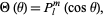 |
(5)
|
where 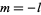 ,
, 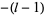 , ..., 0, ...,
, ..., 0, ..., 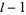 ,
, 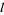 and
and 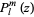 is an associated Legendre polynomial. The spherical harmonics are then defined by combining
is an associated Legendre polynomial. The spherical harmonics are then defined by combining 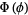 and
and 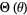 ,
,
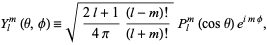 |
(6)
|
where the normalization is chosen such that
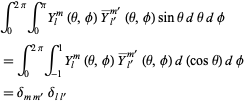 |
(7)
|
(Arfken 1985, p. 681). Here, 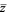 denotes the complex conjugate and
denotes the complex conjugate and 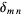 is the Kronecker delta. Sometimes (e.g., Arfken 1985), the Condon-Shortley phase
is the Kronecker delta. Sometimes (e.g., Arfken 1985), the Condon-Shortley phase 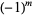 is prepended to the definition of the spherical harmonics.
is prepended to the definition of the spherical harmonics.
The spherical harmonics are sometimes separated into their real and imaginary parts,
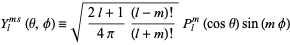 |
(8)
|
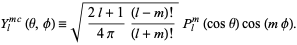 |
(9)
|
The spherical harmonics obey
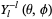 |
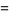 |
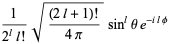 |
(10)
|
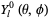 |
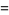 |
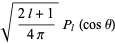 |
(11)
|
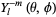 |
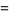 |
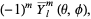 |
(12)
|
where 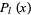 is a Legendre polynomial.
is a Legendre polynomial.
Integrals of the spherical harmonics are given by
 |
(13)
|
where 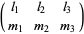 is a Wigner 3j-symbol (which is related to the Clebsch-Gordan coefficients). Special cases include
is a Wigner 3j-symbol (which is related to the Clebsch-Gordan coefficients). Special cases include
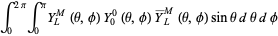 |
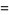 |
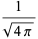 |
(14)
|
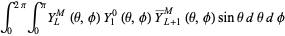 |
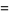 |
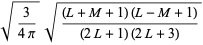 |
(15)
|
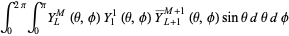 |
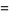 |
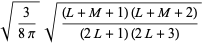 |
(16)
|
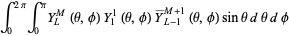 |
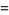 |
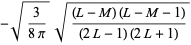 |
(17)
|
(Arfken 1985, p. 700).
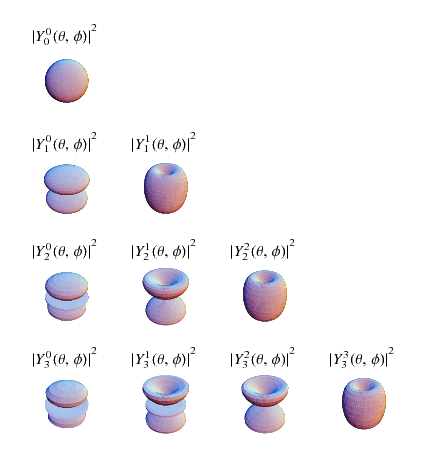
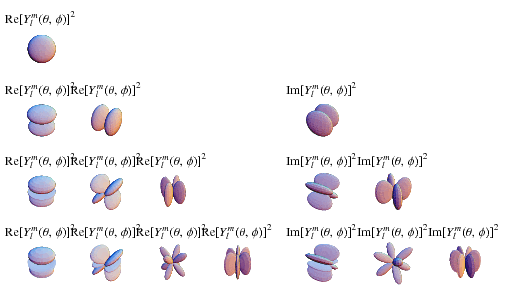
The above illustrations show 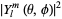 (top),
(top), ![R[Y_l^m(theta,phi)]^2](http://mathworld.wolfram.com/images/equations/SphericalHarmonic/Inline46.gif) (bottom left), and
(bottom left), and ![I[Y_l^m(theta,phi)]^2](http://mathworld.wolfram.com/images/equations/SphericalHarmonic/Inline47.gif) (bottom right). The first few spherical harmonics are
(bottom right). The first few spherical harmonics are
 |
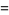 |
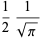 |
(18)
|
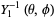 |
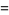 |
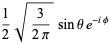 |
(19)
|
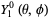 |
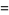 |
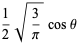 |
(20)
|
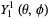 |
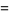 |
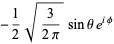 |
(21)
|
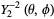 |
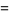 |
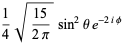 |
(22)
|
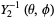 |
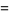 |
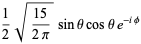 |
(23)
|
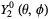 |
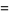 |
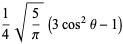 |
(24)
|
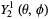 |
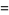 |
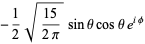 |
(25)
|
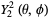 |
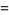 |
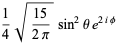 |
(26)
|
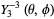 |
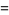 |
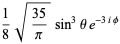 |
(27)
|
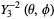 |
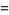 |
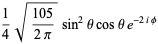 |
(28)
|
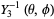 |
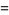 |
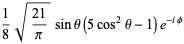 |
(29)
|
 |
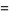 |
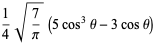 |
(30)
|
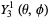 |
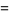 |
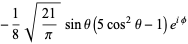 |
(31)
|
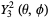 |
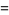 |
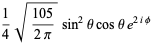 |
(32)
|
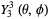 |
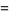 |
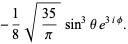 |
(33)
|
Written in terms of Cartesian coordinates,
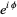 |
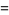 |
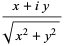 |
(34)
|
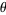 |
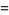 |
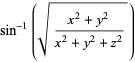 |
(35)
|
 |
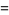 |
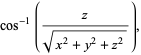 |
(36)
|
so
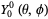 |
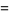 |
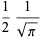 |
(37)
|
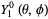 |
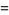 |
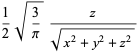 |
(38)
|
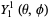 |
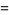 |
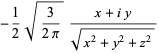 |
(39)
|
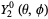 |
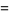 |
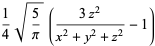 |
(40)
|
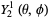 |
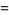 |
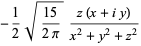 |
(41)
|
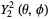 |
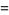 |
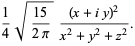 |
(42)
|
The zonal harmonics are defined to be those of the form
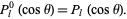 |
(43)
|
The tesseral harmonics are those of the form
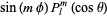 |
(44)
|
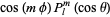 |
(45)
|
for 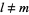 . The sectorial harmonics are of the form
. The sectorial harmonics are of the form
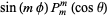 |
(46)
|
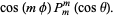 |
(47)
|