Fermat Polynomial
المؤلف:
Koshy, T
المصدر:
Fibonacci and Lucas Numbers with Applications. New York: Wiley, 2001.
الجزء والصفحة:
...
18-9-2019
1605
Fibonacci Polynomial
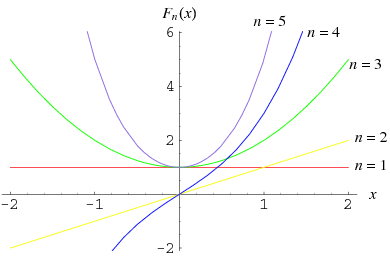
The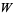 
polynomials obtained by setting 
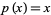and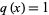 
in the Lucas polynomial sequence. (The corresponding 
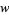polynomials are called Lucas polynomials.) They have explicit formula
 |
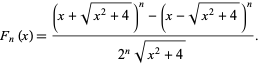(1)
|
The Fibonacci polynomial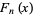 
is implemented in the Wolfram Language as Fibonacci[n, x].
The Fibonacci polynomials are defined by the recurrence relation
 |
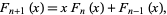(2)
|
with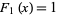 
and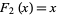 
.
The first few Fibonacci polynomials are
(OEIS A049310).
The Fibonacci polynomials have generating function
The Fibonacci polynomials are normalized so that
 |
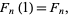(11)
|
where the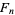 
s are Fibonacci numbers.
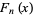is also given by the explicit sum formula
 |
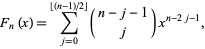(12)
|
where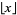 
is the floor function and 
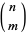is a binomial coefficient.
The derivative of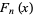 
is given by
 |
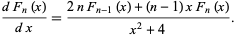(13)
|
The Fibonacci polynomials have the divisibility property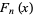 
divides 
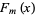iff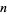 
divides 
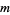. For prime 
, 
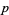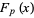is an irreducible polynomial. The zeros of 
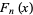are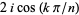 
for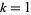 
, ..., 
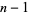. For prime 
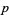, these roots are 
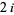times the real part of the roots of the 
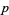th cyclotomic polynomial (Koshy 2001, p. 462).
The identity
 |
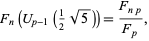(14)
|
for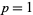 
, 3, ... and 
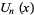a Chebyshev polynomial of the second kind gives the identities
and so on, where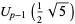 
gives the sequence 4, 11, 29, ... (OEIS A002878).
The Fibonacci polynomials are related to the Morgan-Voyce polynomials by
(Swamy 1968).
REFERENCES:
Koshy, T. Fibonacci and Lucas Numbers with Applications. New York: Wiley, 2001.
Sloane, N. J. A. Sequence A002878/M3420 in "The On-Line Encyclopedia of Integer Sequences."
Swamy, M. N. S. "Further Properties of Morgan-Voyce Polynomials." Fib. Quart. 6, 167-175, 1968.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
