تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Infinite Product
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
13-11-2019
3830
Infinite Product
A product involving an infinite number of terms. Such products can converge. In fact, for positive 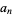 , the product
, the product 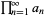 converges to a nonzero number iff
converges to a nonzero number iff 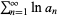 converges.
converges.
Infinite products can be used to define the cosine
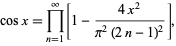 |
(1) |
gamma function
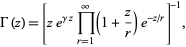 |
(2) |
sine, and sinc function. They also appear in polygon circumscribing,
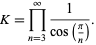 |
(3) |
An interesting infinite product formula due to Euler which relates 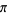 and the
and the 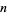 th prime
th prime 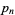 is
is
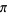 |
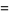 |
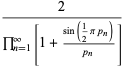 |
(4) |
 |
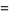 |
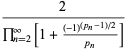 |
(5) |
(Blatner 1997). Knar's formula gives a functional equation for the gamma function 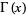 in terms of the infinite product
in terms of the infinite product
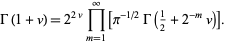 |
(6) |
A regularized product identity is given by
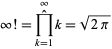 |
(7) |
(Muñoz Garcia and Pérez-Marco 2003, 2008).
Mellin's formula states
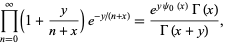 |
(8) |
where 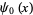 is the digamma function and
is the digamma function and 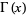 is the gamma function.
is the gamma function.
The following class of products
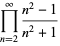 |
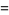 |
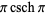 |
(9) |
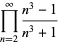 |
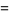 |
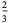 |
(10) |
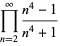 |
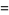 |
![-1/2pisinhpicsc[(-1)^(1/4)pi]csc[(-1)^(3/4)pi]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline24.gif) |
(11) |
 |
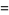 |
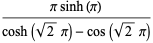 |
(12) |
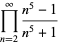 |
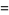 |
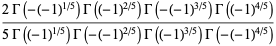 |
(13) |
(Borwein et al. 2004, pp. 4-6), where 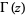 is the gamma function, the first of which is given in Borwein and Corless (1999), can be done analytically. In particular, for
is the gamma function, the first of which is given in Borwein and Corless (1999), can be done analytically. In particular, for 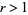 ,
,
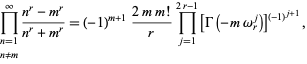 |
(14) |
where 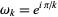 (Borwein et al. 2004, pp. 6-7). It is not known if (13) is algebraic, although it is known to satisfy no integer polynomial with degree less than 21 and Euclidean norm less than
(Borwein et al. 2004, pp. 6-7). It is not known if (13) is algebraic, although it is known to satisfy no integer polynomial with degree less than 21 and Euclidean norm less than 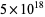 (Borwein et al. 2004, p. 7).
(Borwein et al. 2004, p. 7).
Products of the following form can be done analytically,
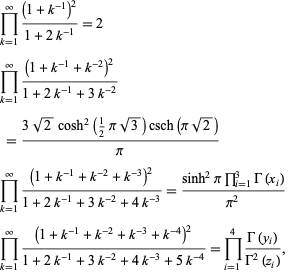 |
(15) |
where 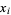 ,
, 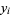 , and
, and 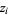 are the roots of
are the roots of
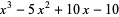 |
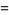 |
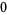 |
(16) |
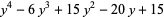 |
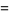 |
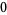 |
(17) |
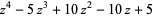 |
 |
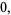 |
(18) |
respectively, can also be done analytically. Note that (17) and (18) were unknown to Borwein and Corless (1999). These are special cases of the result that
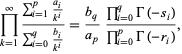 |
(19) |
if 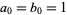 and
and 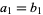 , where
, where 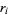 is the
is the 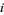 th root of
th root of 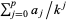 and
and 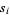 is the
is the 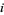 th root of
th root of 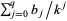 (P. Abbott, pers. comm., Mar. 30, 2006).
(P. Abbott, pers. comm., Mar. 30, 2006).
For 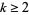 ,
,
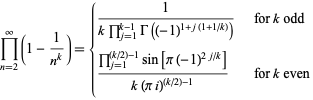 |
(20) |
(D. W. Cantrell, pers. comm., Apr. 18, 2006). The first few explicit cases are
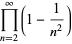 |
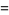 |
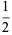 |
(21) |
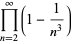 |
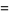 |
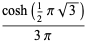 |
(22) |
 |
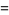 |
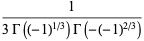 |
(23) |
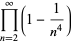 |
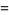 |
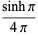 |
(24) |
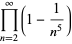 |
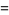 |
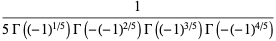 |
(25) |
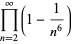 |
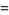 |
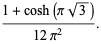 |
(26) |
These are a special case of the general formula
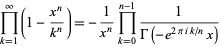 |
(27) |
(Prudnikov et al. 1986, p. 754).
Similarly, for 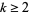 ,
,
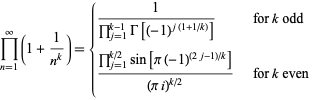 |
(28) |
(D. W. Cantrell, pers. comm., Mar. 29, 2006). The first few explicit cases are
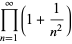 |
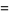 |
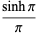 |
(29) |
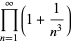 |
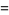 |
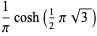 |
(30) |
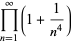 |
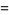 |
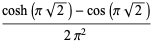 |
(31) |
 |
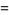 |
![-(sin[(-1)^(1/4)pi]sin[(-1)^(3/4)pi])/(pi^2)](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline86.gif) |
(32) |
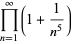 |
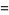 |
![|Gamma[exp(2/5pii)]Gamma[exp(6/5pii)]|^(-2)](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline89.gif) |
(33) |
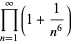 |
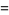 |
![(sinhpi[coshpi-cos(sqrt(3)pi)])/(2pi^3).](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline92.gif) |
(34) |
The d-analog expression
![[infty!]_d=product_(n=3)^infty(1-(2^d)/(n^d))](http://mathworld.wolfram.com/images/equations/InfiniteProduct/NumberedEquation13.gif) |
(35) |
also has closed form expressions,
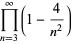 |
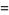 |
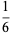 |
(36) |
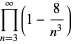 |
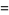 |
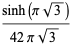 |
(37) |
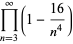 |
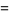 |
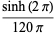 |
(38) |
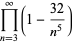 |
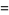 |
![|Gamma[exp(1/5pii)]Gamma[2exp(7/5pii)]|^(-2).](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline104.gif) |
(39) |
General expressions for infinite products of this type include
![product_(n=1)^(infty)[1-(z/n)^(2N)]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline105.gif) |
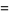 |
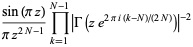 |
(40) |
![product_(n=1)^(infty)[1+(z/n)^(2N)]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline108.gif) |
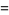 |
![1/(z^(2N))product_(k=1)^(N)|Gamma(ze^(pii[2(k-N)-1]/(2N)))|^(-2)](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline110.gif) |
(41) |
![product_(n=1)^(infty)[1-(z/n)^(2N+1)]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline111.gif) |
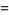 |
![1/(Gamma(1-z)z^(2N))product_(k=1)^(N)|Gamma(ze^(pii[2(k-N)-1]/(2N+1)))|^(-2)](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline113.gif) |
(42) |
![product_(n=1)^(infty)[1+(z/n)^(2N+1)]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline114.gif) |
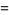 |
 |
(43) |
where 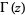 is the gamma function and
is the gamma function and 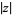 denotes the complex modulus (Kahovec). (40) and (41) can also be rewritten as
denotes the complex modulus (Kahovec). (40) and (41) can also be rewritten as
![product_(n=1)^(infty)[1-(z/n)^(2N)]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline119.gif) |
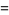 |
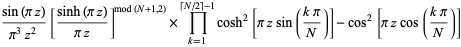 |
(44) |
![product_(n=1)^(infty)[1+(z/n)^(2N)]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline122.gif) |
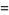 |
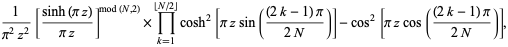 |
(45) |
where 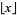 is the floor function,
is the floor function, ![[x]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline126.gif) is the ceiling function, and
is the ceiling function, and 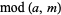 is the modulus of
is the modulus of 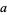 (mod
(mod 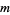 ) (Kahovec).
) (Kahovec).
Infinite products of the form
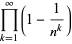 |
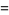 |
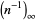 |
(46) |
 |
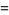 |
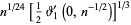 |
(47) |
converge for 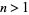 , where
, where 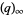 is a q-Pochhammer symbol and
is a q-Pochhammer symbol and 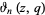 is a Jacobi theta function. Here, the
is a Jacobi theta function. Here, the 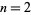 case is exactly the constant
case is exactly the constant 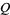 encountered in the analysis of digital tree searching.
encountered in the analysis of digital tree searching.
Other products include
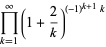 |
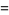 |
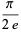 |
(48) |
||
 |
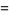 |
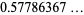 |
(49) |
||
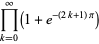 |
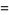 |
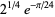 |
(50) |
||
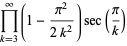 |
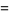 |
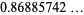 |
 |
 |
(51) |
(OEIS A086056 and A247559; Prudnikov et al. 1986, p. 757). Note that Prudnikov et al. (1986, p. 757) also incorrectly give the product
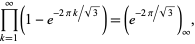 |
(52) |
where 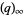 is a q-Pochhammer symbol, as
is a q-Pochhammer symbol, as 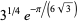 , which differs from the correct result by
, which differs from the correct result by 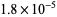 .
.
The following analogous classes of products can also be done analytically (J. Zúñiga, pers. comm., Nov. 9, 2004), where again 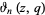 is a Jacobi theta function,
is a Jacobi theta function,
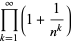 |
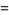 |
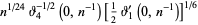 |
(53) |
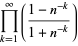 |
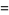 |
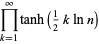 |
(54) |
 |
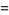 |
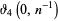 |
(55) |
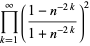 |
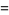 |
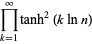 |
(56) |
 |
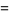 |
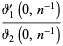 |
(57) |
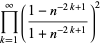 |
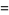 |
![product_(k=1)^(infty)tanh^2[(k-1/2)lnn]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline176.gif) |
(58) |
 |
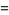 |
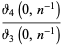 |
(59) |
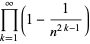 |
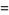 |
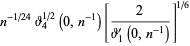 |
(60) |
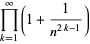 |
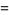 |
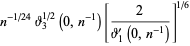 |
(61) |
![product_(k=1)^(infty)[1+(-1)^(k-1)b/(k+a)]](http://mathworld.wolfram.com/images/equations/InfiniteProduct/Inline186.gif) |
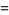 |
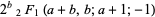 |
(62) |
 |
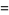 |
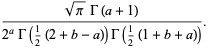 |
(63) |
The first of these can be used to express the Fibonacci factorial constant in closed form.
A class of infinite products derived from the Barnes G-function is given by
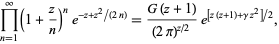 |
(64) |
where 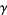 is the Euler-Mascheroni constant. For
is the Euler-Mascheroni constant. For 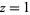 , 2, 3, and 4, the explicit products are given by
, 2, 3, and 4, the explicit products are given by
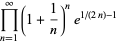 |
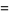 |
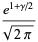 |
(65) |
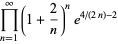 |
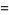 |
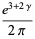 |
(66) |
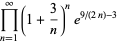 |
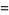 |
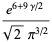 |
(67) |
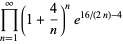 |
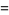 |
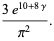 |
(68) |
The interesting identities
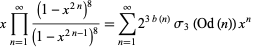 |
(69) |
(Ewell 1995, 2000), where 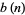 is the exponent of the exact power of 2 dividing
is the exponent of the exact power of 2 dividing 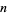 ,
, 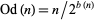 is the odd part of
is the odd part of 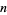 ,
, 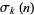 is the divisor function of
is the divisor function of 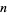 , and
, and
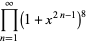 |
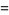 |
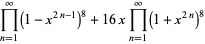 |
(70) |
 |
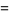 |
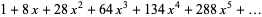 |
(71) |
(OEIS A101127; Jacobi 1829; Ford et al. 1994; Ewell 1998, 2000), the latter of which is known as "aequatio identica satis abstrusa" in the string theory physics literature, arise is connection with the tau function.
An unexpected infinite product involving 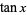 is given by
is given by
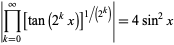 |
(72) |
(Dobinski 1876, Agnew and Walker 1947).
A curious identity first noted by Gosper is given by
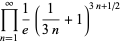 |
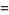 |
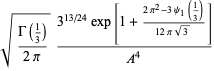 |
(73) |
 |
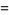 |
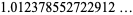 |
(74) |
(OEIS A100072), where 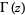 is the gamma function,
is the gamma function, 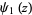 is the trigamma function, and
is the trigamma function, and 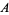 is the Glaisher-Kinkelin constant.
is the Glaisher-Kinkelin constant.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 75, 1972.
Agnew, R. P. and Walker, R. J. "A Trigonometric Infinite Product." Amer. Math. Monthly 54, 206-211, 1947.
Arfken, G. "Infinite Products." §5.11 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 346-351, 1985.
Blatner, D. The Joy of Pi. New York: Walker, p. 119, 1997.
Borwein, J.; Bailey, D.; and Girgensohn, R. "Two Products." §1.2 in Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, pp. 4-7, 2004.
Borwein, J. M. and Corless, R. M. "Emerging Tools for Experimental Mathematics." Amer. Math. Monthly 106, 899-909, 1999.
Dobinski, G. "Product einer unendlichen Factorenreihe." Archiv Math. u. Phys. 59, 98-100, 1876.
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, p. 6, 1981.
Ewell, J. A. "Arithmetical Consequences of a Sextuple Product Identity." Rocky Mtn. J. Math. 25, 1287-1293, 1995.
Ewell, J. A. "A Note on a Jacobian Identity." Proc. Amer. Math. Soc. 126, 421-423, 1998.
Ewell, J. A. "New Representations of Ramanujan's Tau Function." Proc. Amer. Math. Soc. 128, 723-726, 2000.
Finch, S. R. "Kepler-Bouwkamp Constant." §6.3 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 428-429, 2003.
Ford, D.; McKay, J.; and Norton, S. P. "More on Replicable Functions." Commun. Alg. 22, 5175-5193, 1994.
Hansen, E. R. A Table of Series and Products. Englewood Cliffs, NJ: Prentice-Hall, 1975.
Jacobi, C. G. J. "E formulis (7.),(8.) sequitur aequatio identica satis abstrusa: (14.) 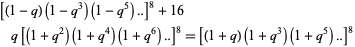 ." Fundamenta Nova Theoriae Functionum Ellipticarum. Königsberg, Germany: Regiomonti, Sumtibus fratrum Borntraeger, 1829. Reprinted in Gesammelte Werke, Band. 1. Providence, RI: Amer. Math. Soc., p. 147, 1969.
." Fundamenta Nova Theoriae Functionum Ellipticarum. Königsberg, Germany: Regiomonti, Sumtibus fratrum Borntraeger, 1829. Reprinted in Gesammelte Werke, Band. 1. Providence, RI: Amer. Math. Soc., p. 147, 1969.
Jeffreys, H. and Jeffreys, B. S. "Infinite Products." §1.14 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 52-53, 1988.
Krantz, S. G. "The Concept of an Infinite Product." §8.1.6 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 104-105, 1999.
Muñoz García, E. and Pérez Marco, R. "The Product Over All Primes is 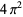 ." Preprint IHES/M/03/34. May 2003. http://inc.web.ihes.fr/prepub/PREPRINTS/M03/Resu/resu-M03-34.html.
." Preprint IHES/M/03/34. May 2003. http://inc.web.ihes.fr/prepub/PREPRINTS/M03/Resu/resu-M03-34.html.
Muñoz García, E. and Pérez Marco, R. "The Product Over All Primes is 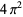 ." Commun. Math. Phys. 277, 69-81, 2008.
." Commun. Math. Phys. 277, 69-81, 2008.
Prudnikov, A. P.; Brychkov, Yu. A.; and Marichev, O. I. "Infinite Products." §6.2 in Integrals and Series, Vol. 1: Elementary Functions. New York: Gordon & Breach, pp. 753-757, 1986.
Ritt, J. F. "Representation of Analytic Functions as Infinite Products." Math. Z. 32, 1-3, 1930.
Sloane, N. J. A. Sequences A048651, A086056, A100072, A100220, A100221, A100222, A101127, and A247559 in "The On-Line Encyclopedia of Integer Sequences."
Whittaker, E. T. and Watson, G. N. §7.5-7.6 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)