Let a convex polygon be inscribed in a circle and divided into triangles from diagonals from one polygon vertex. The sum of the radii of the circles inscribed in these triangles is the same independent of the polygon vertex chosen (Johnson 1929, p. 193).

If a triangle is inscribed in a circle, another circle inside the triangle, a square inside the circle, another circle inside the square, and so on. Then the equation relating the inradius and circumradius of a regular polygon,

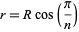(1)

gives the ratio of the radii of the final to initial circles as

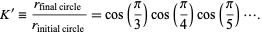(2)

Numerically,

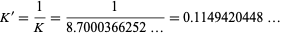(3)

(OEIS A085365), where 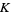 is the corresponding constant for polygon circumscribing. This constant is termed the Kepler-Bouwkamp constant by Finch (2003). Kasner and Newman's (1989) assertion that  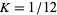is incorrect, as is the value of 0.8700... given by Prudnikov et al. (1986, p. 757).

REFERENCES:

Finch, S. R. "Kepler-Bouwkamp Constant." §6.3 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 428-429, 2003.

Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, 1929.

Kasner, E. and Newman, J. R. Mathematics and the Imagination. Redmond, WA: Microsoft Press, pp. 311-312, 1989.

Pappas, T. "Infinity & Limits." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 180, 1989.

Plouffe, S. "Product(cos(Pi/n),n=3..infinity)." http://pi.lacim.uqam.ca/piDATA/productcos.txt.

Prudnikov, A. P.; Brychkov, Yu. A.; and Marichev, O. I. Integrals and Series, Vol. 1: Elementary Functions. New York: Gordon & Breach, 1986.

Sloane, N. J. A. Sequence A085365 in "The On-Line Encyclopedia of Integer Sequences."