An Euler brick is a cuboid that possesses integer edges 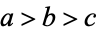 and face diagonals

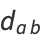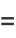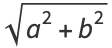			(1)
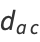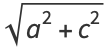			(2)
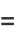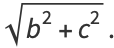			(3)

If the space diagonal is also an integer, the Euler brick is called a perfect cuboid, although no examples of perfect cuboids are currently known.

The smallest Euler brick has sides  and face polyhedron diagonals 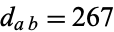, , and 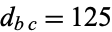, and was discovered by Halcke (1719; Dickson 2005, pp. 497-500). Kraitchik gave 257 cuboids with the odd edge less than 1 million (Guy 1994, p. 174). F. Helenius has compiled a list of the 5003 smallest (measured by the longest edge) Euler bricks. The first few are (240, 117, 44), (275, 252, 240), (693, 480, 140), (720, 132, 85), (792, 231, 160), ... (OEIS A031173, A031174, and A031175).

Interest in this problem was high during the 18th century, and Saunderson (1740) found a parametric solution always giving Euler bricks (but not giving all possible Euler bricks), while in 1770 and 1772, Euler found at least two parametric solutions. Saunderson's solution lets  be a Pythagorean triple, then

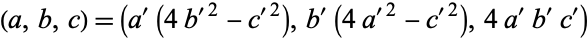(4)

is an Euler brick with face diagonals

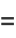			(5)
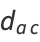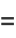			(6)
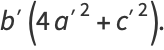			(7)

(Saunderson 1740; Dickson 2005, p. 497).

REFERENCES:

Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, 2005.

Guy, R. K. "Is There a Perfect Cuboid? Four Squares Whose Sums in Pairs Are Square. Four Squares Whose Differences are Square." §D18 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 173-181, 1994.

Halcke, P. Deliciae Mathematicae; oder, Mathematisches sinnen-confect. Hamburg, Germany: N. Sauer, p. 265, 1719.

Leech, J. "The Rational Cuboid Revisited." Amer. Math. Monthly 84, 518-533, 1977. Erratum in Amer. Math. Monthly 85, 472, 1978.

Peterson, I. "MathTrek: Euler Bricks and Perfect Polyhedra." Oct. 23, 1999. https://www.sciencenews.org/sn_arc99/10_23_99/mathland.htm.

Sloane, N. J. A. Sequences A031173, A031174, and A031175 in "The On-Line Encyclopedia of Integer Sequences."

Rathbun, R. L. "Integer Cuboid Search Update." 8 Jan 2001. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0101&L=NMBRTHRY&P=1272.

Saunderson, N. The Elements of Algebra in 10 Books, Vol. 2. Cambridge, England: University Press, pp. 429-431, 1740.

Spohn, W. G. "On the Integral Cuboid." Amer. Math. Monthly 79, 57-59, 1972.

Spohn, W. G. "On the Derived Cuboid." Canad. Math. Bull. 17, 575-577, 1974.

Wells, D. G. The Penguin Dictionary of Curious and Interesting Numbers. London: Penguin, p. 127, 1986.