

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Multigrade Equation
المؤلف:
Chernick, J.
المصدر:
"Ideal Solutions of the Tarry-Escott Problem." Amer. Math. Monthly 44
الجزء والصفحة:
...
3-6-2020
1223
A 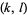 -multigrade equation is a Diophantine equation of the form
-multigrade equation is a Diophantine equation of the form
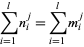 |
(1) |
for 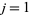 , ...,
, ..., 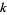 , where
, where 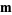 and
and 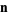 are
are 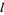 -vectors. Multigrade identities remain valid if a constant is added to each element of
-vectors. Multigrade identities remain valid if a constant is added to each element of 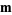 and
and 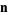 (Madachy 1979), so multigrades can always be put in a form where the minimum component of one of the vectors is 1.
(Madachy 1979), so multigrades can always be put in a form where the minimum component of one of the vectors is 1.
Moessner and Gloden (1944) give a bevy of multigrade equations. Small-order examples are the (2, 3)-multigrade with {1,6,8}" src="https://mathworld.wolfram.com/images/equations/MultigradeEquation/Inline9.gif" style="height:15px; width:76px" /> and
{2,4,9}" src="https://mathworld.wolfram.com/images/equations/MultigradeEquation/Inline10.gif" style="height:15px; width:72px" />:
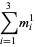 |
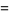 |
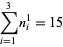 |
(2) |
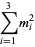 |
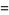 |
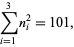 |
(3) |
the (3, 4)-multigrade with {1,5,8,12}" src="https://mathworld.wolfram.com/images/equations/MultigradeEquation/Inline17.gif" style="height:15px; width:98px" /> and
{2,3,10,11}" src="https://mathworld.wolfram.com/images/equations/MultigradeEquation/Inline18.gif" style="height:15px; width:101px" />:
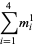 |
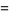 |
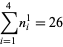 |
(4) |
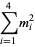 |
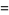 |
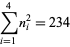 |
(5) |
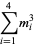 |
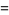 |
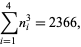 |
(6) |
and the (4, 6)-multigrade with {1,5,8,12,18,19}" src="https://mathworld.wolfram.com/images/equations/MultigradeEquation/Inline28.gif" style="height:15px; width:142px" /> and
{2,3,9,13,16,20}" src="https://mathworld.wolfram.com/images/equations/MultigradeEquation/Inline29.gif" style="height:15px; width:138px" />:
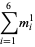 |
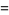 |
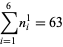 |
(7) |
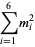 |
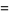 |
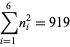 |
(8) |
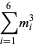 |
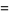 |
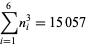 |
(9) |
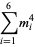 |
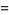 |
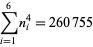 |
(10) |
(Madachy 1979).
A spectacular example with 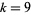 and
and 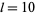 is given by
is given by {+/-12,+/-11881,+/-20231,+/-20885,+/-23738}" src="https://mathworld.wolfram.com/images/equations/MultigradeEquation/Inline44.gif" style="height:15px; width:279px" /> and
{+/-436,+/-11857,+/-20449,+/-20667,+/-23750}" src="https://mathworld.wolfram.com/images/equations/MultigradeEquation/Inline45.gif" style="height:15px; width:290px" /> (Guy 1994), which has sums
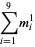 |
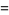 |
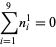 |
(11) |
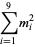 |
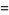 |
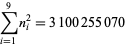 |
(12) |
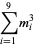 |
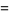 |
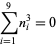 |
(13) |
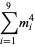 |
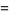 |
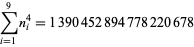 |
(14) |
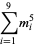 |
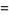 |
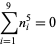 |
(15) |
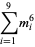 |
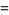 |
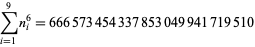 |
(16) |
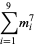 |
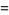 |
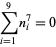 |
(17) |
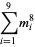 |
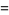 |
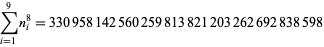 |
(18) |
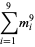 |
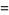 |
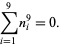 |
(19) |
Rivera considers multigrade equations involving primes, consecutive primes, etc.
Analogous multigrade identities to Ramanujan's fourth power identity of form
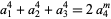 |
(20) |
can also be given for third and fifth powers, the former being
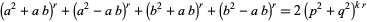 |
(21) |
with 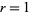 , 2, 3, for any positive integer
, 2, 3, for any positive integer 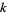 , and where
, and where
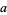 |
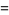 |
![1/2[(p-qi)^k+(p+qi)^k]](https://mathworld.wolfram.com/images/equations/MultigradeEquation/Inline77.gif) |
(22) |
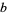 |
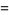 |
![1/2i[(p-qi)^k-(p+qi)^k]](https://mathworld.wolfram.com/images/equations/MultigradeEquation/Inline80.gif) |
(23) |
and the one for fifth powers
^n=2(p^2+pq+q^2)^(hn)](https://mathworld.wolfram.com/images/equations/MultigradeEquation/NumberedEquation4.gif) |
(24) |
for 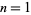 , 3, 5, any positive integer
, 3, 5, any positive integer 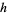 , and where
, and where
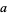 |
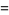 |
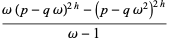 |
(25) |
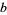 |
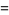 |
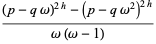 |
(26) |
 |
 |
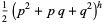 |
(27) |
with 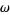 a complex cube root of unity and
a complex cube root of unity and 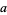 and
and 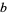 for both cases rational for arbitrary rationals
for both cases rational for arbitrary rationals 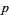 and
and 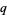 .
.
Multigrade sum-product identities as binary quadratic forms also exist for third, fourth, fifth powers. These are the second of the following pairs.
For third powers with 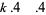 ,
,
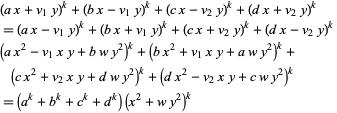 |
(28) |
for 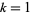 , 3,
, 3, 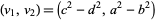 , and
, and 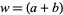 or
or 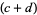 for arbitrary
for arbitrary 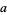 ,
, 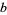 ,
, 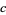 ,
, 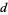 ,
,  , and
, and 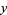 .
.
For fourth powers with 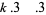 ,
,
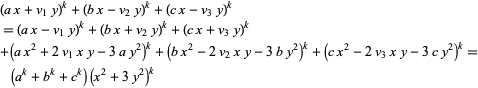 |
(29) |
for 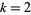 , 4,
, 4, 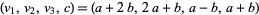 , for arbitrary
, for arbitrary 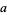 ,
, 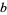 ,
,  ,
, 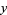 .
.
For fifth powers with 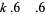 ,
,
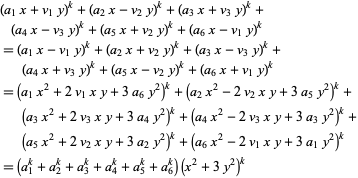 |
(30) |
for 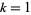 , 2, 3, 4, 5,
, 2, 3, 4, 5, 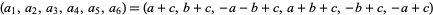 ,
, 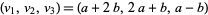 (which are the same
(which are the same 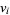 for fourth powers) for arbitrary
for fourth powers) for arbitrary 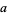 ,
, 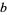 ,
, 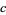 ,
,  ,
, 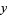 and one for seventh powers that uses
and one for seventh powers that uses 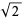 .
.
For seventh powers with 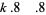 ,
,
 |
(31) |
for 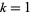 to 7,
to 7, 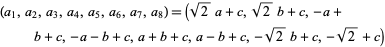 ,
, 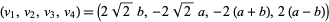 , for arbitrary,
, for arbitrary, 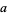 ,
, 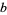 ,
, 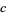 ,
,  ,
, 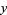 (Piezas 2006).
(Piezas 2006).
A multigrade 5-parameter binary quadratic form identity exists for 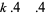 with
with 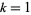 , 2, 3, 5. Given arbitrary variables
, 2, 3, 5. Given arbitrary variables 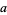 ,
, 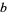 ,
, 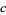 ,
,  ,
, 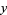 and defining
and defining 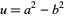 and
and 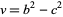 , then
, then
![[(-a+b+c)x^2+2(cu-bv)xy-(a+b+c)uvy^2]^k+[(a-b+c)x^2+2(cu+bv)xy+(a+b-c)uvy^2]^k+[(a+b-c)x^2+2(-cu-bv)xy+(a-b+c)uvy^2]^k+[-(a+b+c)x^2+2(-cu+bv)xy+(-a+b+c)uvy^2]^k-[-(a+b+c)x^2+2(-bu+av)xy+(a+b-c)uvy^2]^k-[(a+b-c)x^2+2(bu-av)xy-(a+b+c)uvy^2]^k-[(a-b+c)x^2+2(-bu-av)xy+(-a+b+c)uvy^2]^k-[(-a+b+c)x^2+2(bu+av)xy+(a-b+c)uvy^2]^k=0](https://mathworld.wolfram.com/images/equations/MultigradeEquation/NumberedEquation9.gif) |
(32) |
for 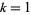 , 2, 3, 5 (T. Piezas, pers. comm., Apr. 27, 2006).
, 2, 3, 5 (T. Piezas, pers. comm., Apr. 27, 2006).
Chernick (1937) gave a multigrade binary quadratic form parametrization to 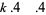 for
for 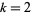 , 4, 6 given by
, 4, 6 given by
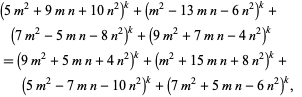 |
(33) |
an equation which depends on finding solutions to 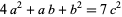 .
.
Sinha (1966ab) gave a multigrade binary quadratic form parametrization to 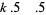 for
for 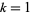 , 3, 5, 7 given by
, 3, 5, 7 given by
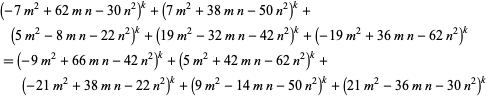 |
(34) |
which depended on solving the system 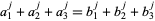 for
for 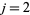 and 4 with
and 4 with 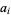 and
and 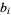 satisfying certain other conditions.
satisfying certain other conditions.
Sinha (1966ab), using a result of Letac, also gave a multigrade parametrization to 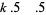 for
for 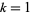 , 2, 4, 6, 8 given by
, 2, 4, 6, 8 given by
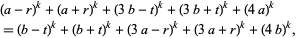 |
(35) |
where 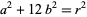 and
and 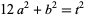 . One nontrivial solution can be given by
. One nontrivial solution can be given by 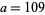 ,
, 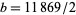 , and Sinha and Smyth proved in 1990 that there are an infinite number of distinct nontrivial solutions.
, and Sinha and Smyth proved in 1990 that there are an infinite number of distinct nontrivial solutions.
REFERENCES:
Chernick, J. "Ideal Solutions of the Tarry-Escott Problem." Amer. Math. Monthly 44, 62600633, 1937.
Gloden, A. Mehrgeradige Gleichungen. Groningen, Netherlands: Noordhoff, 1944.
Gloden, A. "Sur la multigrade 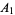 ,
, 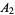 ,
, 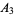 ,
, 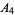 ,
, 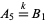 ,
, 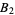 ,
, 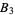 ,
, 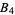 ,
, 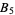 (
(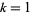 , 3, 5, 7)." Revista Euclides 8, 383-384, 1948.
, 3, 5, 7)." Revista Euclides 8, 383-384, 1948.
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 143, 1994.
Kraitchik, M. "Multigrade." §3.10 in Mathematical Recreations. New York: W. W. Norton, p. 79, 1942.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 171-173, 1979.
Moessner, A. and Gloden, A. "Einige Zahlentheoretische Untersuchungen und Resultate." Bull. Sci. École Polytech. de Timisoara 11, 196-219, 1944.
Piezas, T. "Ramanujan and Fifth Power Identities." https://www.geocities.com/titus_piezas/Ramfifth.html.
Piezas, T. "Binary Quadratic Forms as Equal Sums of Like Powers." https://www.geocities.com/titus_piezas/Binary_quad.html.
Rivera, C. "Problems & Puzzles: Puzzle 065-Multigrade Relations." https://www.primepuzzles.net/puzzles/puzz_065.htm.
Sinha, T. "On the Tarry-Escott Problem." Amer. Math. Monthly 73, 280-285, 1966a.
Sinha, T. "Some System of Diophantine Equations of the Tarry-Escott Type." J. Indian Math. Soc. 30, 15-25, 1966b.