A divisor, also called a factor, of a number 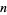 is a number  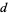which divides  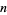(written 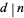). For integers, only positive divisors are usually considered, though obviously the negative of any positive divisor is itself a divisor. A list of (positive) divisors of a given integer  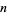may be returned by the Wolfram Language function Divisors[n].

Sums and products are commonly taken over only some subset of values that are the divisors of a given number. Such a sum would then be denoted, for example,

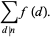(1)

Such sums are implemented in the Wolfram Language as DivisorSum[n, form, cond].

The following tables lists the divisors of the first few positive integers (OEIS A027750).

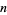	divisors
1	1
2	1, 2
3	1, 3
4	1, 2, 4
5	1, 5
6	1, 2, 3, 6
7	1, 7
8	1, 2, 4, 8
9	1, 3, 9
10	1, 2, 5, 10
11	1, 11
12	1, 2, 3, 4, 6, 12
13	1, 13
14	1, 2, 7, 14
15	1, 3, 5, 15

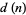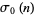The total number of divisors for a given number  (variously written , , or 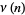) can be found as follows. Write a number in terms of its prime factorization

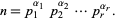(2)

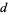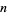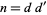For any divisor  of ,  where

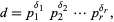(3)

so

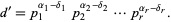(4)

Now, 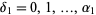, so there are  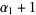possible values. Similarly, for 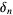, there are  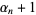possible values, so the total number of divisors  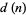of 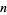 is given by

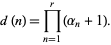(5)

The product of divisors can be found by writing the number 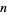 in terms of all possible products

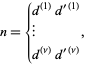(6)

so

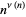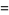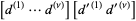			(7)
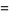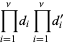			(8)
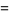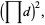			(9)

and

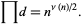(10)

The geometric mean of divisors is

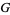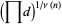			(11)
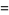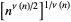			(12)
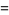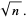			(13)

The arithmetic mean is

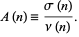(14)

The harmonic mean is

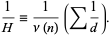(15)

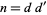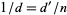But , so  and

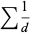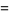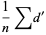			(16)
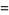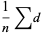			(17)
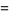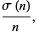			(18)

and we have

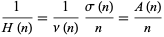(19)

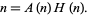(20)

Given three integers chosen at random, the probability that no common factor will divide them all is

(21)

where 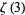 is Apéry's constant.

The smallest numbers having exactly 0, 1, 2, ... divisors (other than 1) are 1, 2, 4, 6, 16, 12, 64, 24, 36, ... (OEIS A005179; Minin 1883-84; Grost 1968; Roberts 1992, p. 86; Dickson 2005, pp. 51-52). Fontené (1902) and Chalde (1903) showed that if 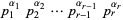 is the prime factorization of the least number with a given number of divisors, then (1)  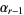is prime, (2)  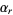is prime except for the number  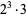which has 8 divisors (Dickson 2005, p. 52).

Let 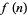 be the number of elements in the greatest subset of  such that none of its elements are divisible by two others. For 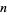 sufficiently large,

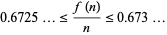(22)

(Le Lionnais 1983, Lebensold 1976/1977).

REFERENCES:

Chalde. Nouv. Ann. Math. 3, 471-473, 1903.

Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, 2005.

Fontené, G. Nouv. Ann. Math. 2, 288, 1902.

Grost, M. E. "The Smallest Number with a Given Number of Divisors." Amer. Math. Monthly 75, 725-729, 1968.

Guy, R. K. "Solutions of 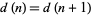." §B18 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 73-75, 1994.

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 43, 1983.

Lebensold, K. "A Divisibility Problem." Studies Appl. Math. 56, 291-294, 1976/1977.

Minin, A. P. Math. Soc. Moscow 11, 632, 1883-84.

Nagell, T. "Divisors." §1 in Introduction to Number Theory. New York: Wiley, pp. 11-12, 1951.

Roberts, J. The Lure of the Integers. Washington, DC: Math. Assoc. Amer., 1992.

Sloane, N. J. A. Sequences A005179/M1026 and A027750 in "The On-Line Encyclopedia of Integer Sequences."