

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Dedekind Sum
المؤلف:
Apostol, T. M.
المصدر:
Ch. 12 in Introduction to Analytic Number Theory. New York: Springer-Verlag, 1976.
الجزء والصفحة:
...
17-8-2020
2053
Given relatively prime integers 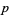 and
and 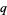 (i.e.,
(i.e., 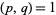 ), the Dedekind sum is defined by
), the Dedekind sum is defined by
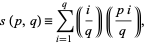 |
(1) |
where
|
(2) |
with 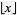 the floor function.
the floor function. 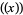 is an odd function since
is an odd function since 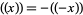 and is periodic with period 1. The Dedekind sum is meaningful even if
and is periodic with period 1. The Dedekind sum is meaningful even if 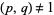 , so the relatively prime restriction is sometimes dropped (Apostol 1997, p. 72). The symbol
, so the relatively prime restriction is sometimes dropped (Apostol 1997, p. 72). The symbol 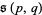 is sometimes used instead of
is sometimes used instead of 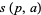 (Beck 2000).
(Beck 2000).
The Dedekind sum can also be expressed in the form
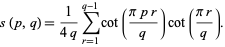 |
(3) |
If 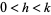 , let
, let 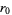 ,
, 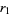 , ...,
, ..., 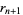 denote the remainders in the Euclidean algorithm given by
denote the remainders in the Euclidean algorithm given by
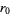 |
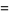 |
 |
(4) |
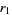 |
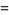 |
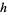 |
(5) |
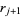 |
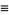 |
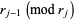 |
(6) |
for 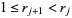 and
and 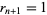 . Then
. Then
|
(7) |
(Apostol 1997, pp. 72-73).
In general, there is no simple formula for closed-form evaluation of 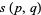 , but some special cases are
, but some special cases are
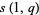 |
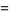 |
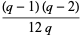 |
(8) |
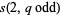 |
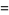 |
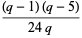 |
(9) |
(Apostol 1997, p. 62). Apostol (1997, p. 73) gives the additional special cases
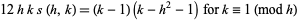 |
(10) |
![12hks(h,k)=(k-2)[k-1/2(h^2+1)] for k=2 (mod h)](https://mathworld.wolfram.com/images/equations/DedekindSum/NumberedEquation6.gif) |
(11) |
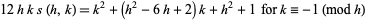 |
(12) |
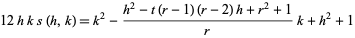 |
(13) |
for 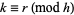 and
and 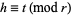 , where
, where 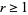 and
and 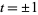 . Finally,
. Finally,
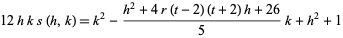 |
(14) |
for 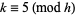 and
and 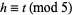 , where
, where 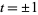 or
or 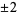 .
.
Dedekind sums obey 2-term
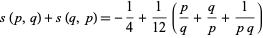 |
(15) |
(Dedekind 1953; Rademacher and Grosswald 1972; Pommersheim 1993; Apostol 1997, pp. 62-64) and 3-term
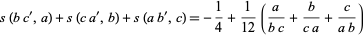 |
(16) |
(Rademacher 1954), reciprocity laws, where 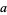 ,
, 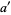 ;
; 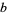 ,
, 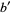 ; and
; and 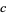 ,
, 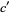 are pairwise relatively prime, and
are pairwise relatively prime, and
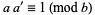 |
(17) |
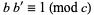 |
(18) |
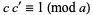 |
(19) |
(Pommersheim 1993).
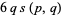 is an integer (Rademacher and Grosswald 1972, p. 28), and if
is an integer (Rademacher and Grosswald 1972, p. 28), and if 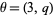 , then
, then
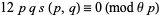 |
(20) |
and
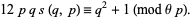 |
(21) |
In addition, 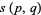 satisfies the congruence
satisfies the congruence
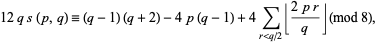 |
(22) |
which, if 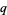 is odd, becomes
is odd, becomes
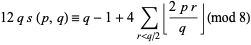 |
(23) |
(Apostol 1997, pp. 65-66). If 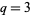 , 5, 7, or 13, let
, 5, 7, or 13, let 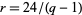 , let integers
, let integers 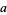 ,
, 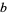 ,
, 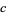 ,
, 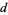 be given with
be given with 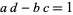 such that
such that 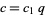 and
and 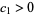 , and let
, and let
|
(24) |
Then 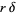 is an even integer (Apostol 1997, pp. 66-69).
is an even integer (Apostol 1997, pp. 66-69).
Let 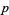 ,
, 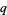 ,
, 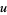 ,
, 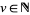 with
with 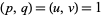 (i.e., are pairwise relatively prime), then the Dedekind sums also satisfy
(i.e., are pairwise relatively prime), then the Dedekind sums also satisfy
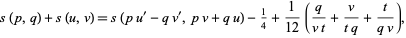 |
(25) |
where 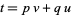 , and
, and 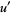 ,
, 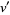 are any integers such that
are any integers such that 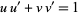 (Pommersheim 1993).
(Pommersheim 1993).
If 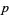 is prime, then
is prime, then
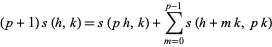 |
(26) |
(Dedekind 1953; Apostol 1997, p. 73). Moreover, it has been beautifully generalized by Knopp (1980).
REFERENCES:
Apostol, T. M. "Properties of Dedekind Sums," "The Reciprocity Law for Dedekind Sums," and "Congruence Properties of Dedekind Sums." §3.7-3.9 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 52 and 61-69, 1997.
Apostol, T. M. Ch. 12 in Introduction to Analytic Number Theory. New York: Springer-Verlag, 1976.
Beck, M. "Dedekind Cotangent Sums" 7 Dec 2001. https://arxiv.org/abs/math.NT/0112077.
Dedekind, R. "Erlauterungen zu den Fragmenten, XXVIII." In The Collected Works of Bernhard Riemann. New York: Dover, pp. 466-478, 1953.
Iseki, S. "The Transformation Formula for the Dedekind Modular Function and Related Functional Equations." Duke Math. J. 24, 653-662, 1957.
Knopp, M. I. "Hecke Operators and an Identity for Dedekind Sums." J. Number Th. 12, 2-9, 1980.
Pommersheim, J. "Toric Varieties, Lattice Points, and Dedekind Sums." Math. Ann. 295, 1-24, 1993.
Rademacher, H. "Generalization of the Reciprocity Formula for Dedekind Sums." Duke Math. J. 21, 391-398, 1954.
Rademacher, H. and Grosswald, E. Dedekind Sums. Washington, DC: Math. Assoc. Amer., 1972.
Rademacher, H. and Whiteman, A. L. "Theorems on Dedekind Sums." Amer. J. Math. 63, 377-407, 1941.