



تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Totient Summatory Function
المؤلف:
DeKoninck, J.-M. and Ivić, A.
المصدر:
Topics in Arithmetical Functions: Asymptotic Formulae for Sums of Reciprocals of Arithmetical Functions and Related Fields. Amsterdam, Netherlands: North-Holland, 1980.
الجزء والصفحة:
...
28-8-2020
1706
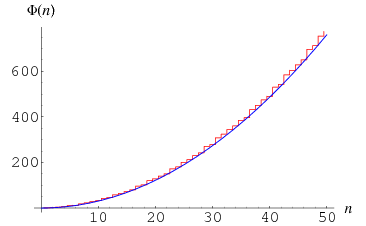
The summatory function 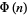 of the totient function
of the totient function 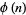 is defined by
is defined by
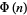 |
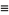 |
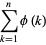 |
(1) |
 |
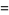 |
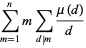 |
(2) |
 |
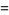 |
 |
(3) |
 |
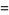 |
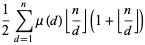 |
(4) |
(Hardy and Wright 1979, p. 268), plotted as the red curve above. The first values of 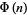 are 1, 2, 4, 6, 10, 12, 18, 22, 28, ... (OEIS A002088).
are 1, 2, 4, 6, 10, 12, 18, 22, 28, ... (OEIS A002088).
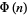 has the asymptotic series
has the asymptotic series
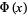 |
 |
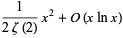 |
(5) |
 |
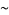 |
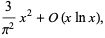 |
(6) |
where 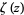 is the Riemann zeta function (Perrot 1881; Nagell 1951, p. 131; Hardy and Wright 1979, p. 268; blue curve above). An improved asymptotic estimate due to Walfisz (1963) is given by
is the Riemann zeta function (Perrot 1881; Nagell 1951, p. 131; Hardy and Wright 1979, p. 268; blue curve above). An improved asymptotic estimate due to Walfisz (1963) is given by
![Phi(x)∼(3x^2)/(pi^2)+O[x(lnx)^(2/3)(lnlnx)^(4/3)].](https://mathworld.wolfram.com/images/equations/TotientSummatoryFunction/NumberedEquation1.gif) |
(7) |
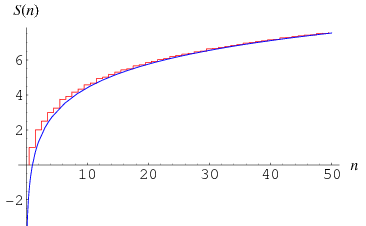
Consider the summatory function of 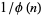 ,
,
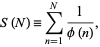 |
(8) |
plotted as the red curve above. For 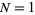 , 2, ..., the first few terms are 1, 2, 5/2, 3, 13/4, 15/4, 47/12, 25/6, ... (OEIS A028415 and A048049). The sum diverges as
, 2, ..., the first few terms are 1, 2, 5/2, 3, 13/4, 15/4, 47/12, 25/6, ... (OEIS A028415 and A048049). The sum diverges as 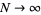 , but Landau (1900) showed that the asymptotic behavior is given by
, but Landau (1900) showed that the asymptotic behavior is given by
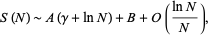 |
(9) |
where 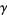 is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant,
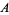 |
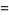 |
![sum_(k=1)^(infty)([mu(k)]^2)/(kphi(k))](https://mathworld.wolfram.com/images/equations/TotientSummatoryFunction/Inline30.gif) |
(10) |
 |
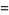 |
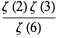 |
(11) |
 |
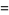 |
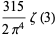 |
(12) |
 |
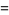 |
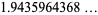 |
(13) |
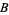 |
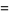 |
![sum_(k=1)^(infty)([mu(k)]^2lnk)/(kphi(k))](https://mathworld.wolfram.com/images/equations/TotientSummatoryFunction/Inline42.gif) |
(14) |
 |
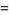 |
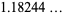 |
(15) |
(OEIS A082695), 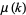 is the Möbius function,
is the Möbius function, 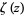 is the Riemann zeta function, and
is the Riemann zeta function, and 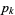 is the
is the 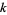 th prime (Landau 1900; Halberstam and Richert 1974, pp. 110-111; DeKoninck and Ivić 1980, pp. 1-3; Finch 2003, p. 116; Havil 2003, p. 115; Dickson 2005).
th prime (Landau 1900; Halberstam and Richert 1974, pp. 110-111; DeKoninck and Ivić 1980, pp. 1-3; Finch 2003, p. 116; Havil 2003, p. 115; Dickson 2005).
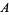 and
and 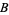 can also be written as
can also be written as
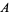 |
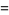 |
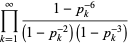 |
(16) |
 |
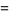 |
![product_(k=1)^(infty)[1+1/(p_k(p_k-1))]](https://mathworld.wolfram.com/images/equations/TotientSummatoryFunction/Inline57.gif) |
(17) |
and
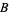 |
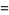 |
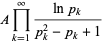 |
(18) |
 |
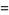 |
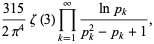 |
(19) |
respectively, making these constants similar in form to Artin's constant (Finch 2003, pp. 116-117).
The sum
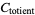 |
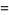 |
 |
(20) |
 |
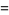 |
![zeta(2)product_(p)[1+1/(p^2(p-1))]](https://mathworld.wolfram.com/images/equations/TotientSummatoryFunction/Inline69.gif) |
(21) |
 |
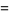 |
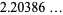 |
(22) |
(OEIS A118262) is sometimes known as the totient constant (Niklasch), where
![product_(p)[1+1/(p^2(p-1))]=1.33978...](https://mathworld.wolfram.com/images/equations/TotientSummatoryFunction/NumberedEquation4.gif) |
(23) |
(OEIS A065483) and the products are taken over the primes 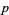 .
.
REFERENCES:
DeKoninck, J.-M. and Ivić, A. Topics in Arithmetical Functions: Asymptotic Formulae for Sums of Reciprocals of Arithmetical Functions and Related Fields. Amsterdam, Netherlands: North-Holland, 1980.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 113-158, 2005.
Finch, S. R. "Euler Totient Constants." §2.7 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 115-119, 2003.
Halberstam, H. and Richert, H.-E. Sieve Methods. New York: Academic Press, 1974.
Hardy, G. H. and Wright, E. M. "The Average Order of 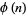 ." §18.5 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 268-269, 1979.
." §18.5 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 268-269, 1979.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.
Landau, E. "Über die zahlentheoretische Function 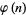 und ihre Beziehung zum Goldbachschen Satz." Nachr. Königlichen Ges. Wiss. Göttingen, Math.-Phys. Klasse, 177-186, 1900. Werke, Vol. 1 (Ed. L. Mirsky, I. J. Schoenberg, W. Schwarz, and H. Wefelscheid). Thales Verlag, pp. 106-115, 1983. Mitrinović, D. S. and Sándor, J. §I.27 in Handbook of Number Theory. Dordrecht, Netherlands: Kluwer, 1995.
und ihre Beziehung zum Goldbachschen Satz." Nachr. Königlichen Ges. Wiss. Göttingen, Math.-Phys. Klasse, 177-186, 1900. Werke, Vol. 1 (Ed. L. Mirsky, I. J. Schoenberg, W. Schwarz, and H. Wefelscheid). Thales Verlag, pp. 106-115, 1983. Mitrinović, D. S. and Sándor, J. §I.27 in Handbook of Number Theory. Dordrecht, Netherlands: Kluwer, 1995.
Nagell, T. "Relatively Prime Numbers. Euler's 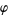 -Function." §8 in Introduction to Number Theory. New York: Wiley, pp. 23-26, 1951.
-Function." §8 in Introduction to Number Theory. New York: Wiley, pp. 23-26, 1951.
Niklasch, G. "Some Number-Theoretical Constants." https://www.gn-50uma.de/alula/essays/Moree/Moree.en.shtml.
Perrot, J. 1811. Quoted in Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, p. 126, 2005.
Sloane, N. J. A. Sequences A028415, A048049, A065483, A082695, A085609, A098468, and A118262 in "The On-Line Encyclopedia of Integer Sequences."
Stephens, P. J. "Prime Divisor of Second-Order Linear Recurrences, I." J. Number Th. 8, 313-332, 1976.
Walfisz, A. Ch. 5 in Weyl'sche Exponentialsummen in der neueren Zahlentheorie. Berlin: Deutscher Verlag der Wissenschaften, 1963.