The factorization of a number into its constituent primes, also called prime decomposition. Given a positive integer 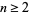, the prime factorization is written

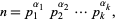where the 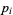s are the  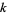prime factors, each of order 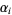. Each factor  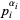is called a primary. Prime factorization can be performed in the Wolfram Language using the command FactorInteger[n], which returns a list of  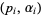pairs.

Through his invention of the Pratt certificate, Pratt (1975) became the first to establish that prime factorization lies in the complexity class NP.

The following Wolfram Language code can be used to give a nicely typeset form of a number :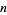

  FactorForm[n_?NumberQ, fac_:Automatic] :=
    Times @@ (HoldForm[Power[##]]& @@@
      FactorInteger[n, fac])

The first few prime factorizations (the number 1, by definition, has a prime factorization of "1") are given in the following table.

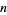	prime factorization		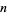prime factorization
1	1	11	11
2	2	12
3	3	13	13
4		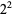14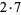
5	5	15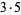
6		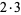16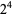
7	7	17	17
8		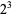18
9		19	19
10		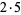20

The number of digits in the prime factorization of 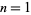, 2, ..., are 1, 1, 1, 2, 1, 2, 1, 2, 2, 2, 2, 3, (OEIS A050252).

In general, prime factorization is a difficult problem, and many sophisticated prime factorization algorithms have been devised for special types of numbers.

Integers can also be factored over the Gaussian primes. For example, the following table gives the Gaussian integer factorizations for the first few positive integers.

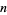	factorization
1	1
2
3	3
4
5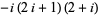
6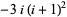
7	7
8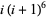
9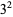
10

Interestingly, prime numbers 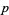 equal to 1 (mod 4) can always by factored into Gaussian primes in the form

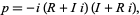where the real and imaginary parts are inverted in the two parts, while prime numbers equal to 3 (mod 4) cannot be factored into Gaussian primes. This is directly related to Fermat's 4n+1 theorem.

REFERENCES:

Dickson, L. E. "Factor Tables, Lists of Primes." Ch. 13 in History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 347-356, 2005.

Glaisher, J. Factor Tables for the Sixth Million: Containing the Least Factor of Every Number Not Divisible by 2, 3, or 5 between 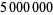 and 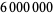. London: Taylor and Francis, 1883.

Lehmer, D. N. Factor Table for the First Ten Millions, Containing the Smallest Factor of Every Number Not Divisible by 2, 3, 5 or 7 Between the Limits 0 and 10017000. Washington, DC: Carnegie Institution of Washington, No. 105, 1909.

Lehmer, D. N. List of Prime Numbers from 1 to 10006721. Washington, DC: Carnegie Institution, 1914.

Peters, J.; Lodge, A.; Ternouth, E. J.; and Gifford, E. Factor Table: Giving the Complete Decomposition of All Numbers Less than 100000. London: British Association for the Advancement of Science, 1935.

Pratt, V. "Every Prime Has a Succinct Certificate." SIAM J. Comput. 4, 214-220, 1975.