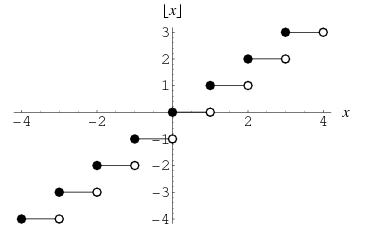
The floor function 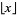, also called the greatest integer function or integer value (Spanier and Oldham 1987), gives the largest integer less than or equal to . The name and symbol for the floor function were coined by K. E. Iverson (Graham et al. 1994).

Unfortunately, in many older and current works (e.g., Honsberger 1976, p. 30; Steinhaus 1999, p. 300; Shanks 1993; Ribenboim 1996; Hilbert and Cohn-Vossen 1999, p. 38; Hardy 1999, p. 18), the symbol  is used instead of 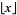 (Graham et al. 1994, p. 67). In fact, this notation harks back to Gauss in his third proof of quadratic reciprocity in 1808. However, because of the elegant symmetry of the floor function and ceiling function symbols  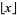and , and because  is such a useful symbol when interpreted as an Iverson bracket, the use of  to denote the floor function should be deprecated. In this work, the symbol  is used to denote the nearest integer function since it naturally falls between the 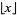 and  symbols.

Min   Max       Re       Im

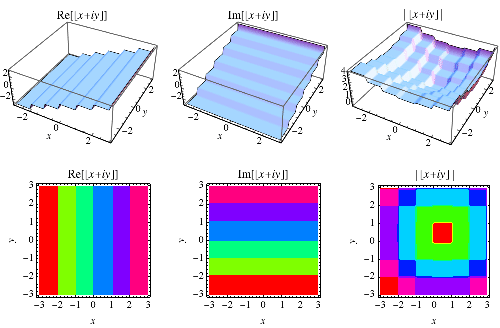The floor function is implemented in the Wolfram Language as Floor[z], where it is generalized to complex values of 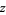 as illustrated above.

Since usage concerning fractional part/value and integer part/value can be confusing, the following table gives a summary of names and notations used. Here, S&O indicates Spanier and Oldham (1987).

notation	name	S&O	Graham et al.	Wolfram Language
	ceiling function	--	ceiling, least integer	Ceiling[x]
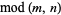	congruence	--	--	Mod[m, n]
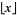	floor function		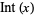floor, greatest integer, integer part	Floor[x]
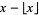	fractional value		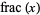fractional part or {x}" src="https://mathworld.wolfram.com/images/equations/FloorFunction/Inline19.gif" style="height:15px; width:17px" />	SawtoothWave[x]
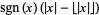	fractional part		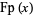no name	FractionalPart[x]
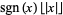	integer part		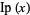no name	IntegerPart[x]
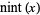	nearest integer function	--	--	Round[x]
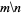	quotient	--	--	Quotient[m, n]

The floor function satisfies the identity

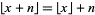(1)

for all integers .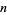

A number of geometric-like sequences with a floor function in the numerator can be done analytically. For instance, sums of the form

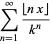(2)

can be done analytically for rational . For  a unit fraction,

(3)

Sums of this form lead to Devil's staircase-like behavior.

For irrational , continued fraction convergents 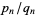, and ,

{|_nalpha_| for n<q_(N+1); |_nalpha_|+(-1)^N for n=q_(N+1) " src="https://mathworld.wolfram.com/images/equations/FloorFunction/NumberedEquation4.gif" style="height:42px; width:249px" />

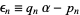(4)

(Borwein et al. 2004, p. 12). This leads to the rather amazing result relating sums of the floor function of multiples of 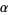 to the continued fraction of  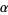by

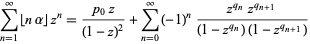(5)

(Mahler 1929; Borwein et al. 2004, p. 12).

REFERENCES:

Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.

Croft, H. T.; Falconer, K. J.; and Guy, R. K. Unsolved Problems in Geometry. New York: Springer-Verlag, p. 2, 1991.

Graham, R. L.; Knuth, D. E.; and Patashnik, O. "Integer Functions." Ch. 3 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 67-101, 1994.

Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.

Hilbert, D. and Cohn-Vossen, S. Geometry and the Imagination. New York: Chelsea, 1999.

Honsberger, R. Mathematical Gems II. Washington, DC: Math. Assoc. Amer., 1976.

Iverson, K. E. A Programming Language. New York: Wiley, p. 12, 1962.

Mahler, K. "Arithmetische Eigenschaften der Lösungen einer Klasse von Funktionalgleichungen." Math. Ann. 101, 342-366, 1929.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 180-182, 1996.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 14, 1993.

Spanier, J. and Oldham, K. B. "The Integer-Value Int() and Fractional-Value frac() Functions." Ch. 9 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 71-78, 1987.

Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, 1999.