

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Multiplicative Persistence
المؤلف:
Beeler, M. Item 56 in Beeler, M.; Gosper, R. W.; and Schroeppel, R.
المصدر:
HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239
الجزء والصفحة:
...
15-11-2020
2636
Multiply all the digits of a number 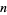 by each other, repeating with the product until a single digit is obtained. The number of steps required is known as the multiplicative persistence, and the final digit obtained is called the multiplicative digital root of
by each other, repeating with the product until a single digit is obtained. The number of steps required is known as the multiplicative persistence, and the final digit obtained is called the multiplicative digital root of 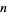 .
.
For example, the sequence obtained from the starting number 9876 is (9876, 3024, 0), so 9876 has an multiplicative persistence of two and a multiplicative digital root of 0. The multiplicative persistences of the first few positive integers are 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 1, 1, ... (OEIS A031346). The smallest numbers having multiplicative persistences of 1, 2, ... are 10, 25, 39, 77, 679, 6788, 68889, 2677889, 26888999, 3778888999, 277777788888899, ... (OEIS A003001; Wells 1986, p. 78). There is no number 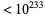 with multiplicative persistence
with multiplicative persistence 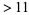 (Carmody 2001; updating Wells 1986, p. 78). It is conjectured that the maximum number lacking the digit 1 with persistence 11 is
(Carmody 2001; updating Wells 1986, p. 78). It is conjectured that the maximum number lacking the digit 1 with persistence 11 is
 |
There is a stronger conjecture that there is a maximum number lacking the digit 1 for each persistence 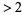 .
.
The maximum multiplicative persistence in base 2 is 1. It is conjectured that all powers of 2 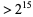 contain a 0 in base 3, which would imply that the maximum persistence in base 3 is 3 (Guy 1994).
contain a 0 in base 3, which would imply that the maximum persistence in base 3 is 3 (Guy 1994).
The multiplicative persistence of an 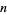 -digit number is also called its number length. The maximum lengths for
-digit number is also called its number length. The maximum lengths for 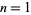 -, 2-, 3-, ..., digit numbers are 0, 4, 5, 6, 7, 7, 8, 9, 9, 10, 10, 10, ... (OEIS A014553; Beeler 1972; Gottlieb 1969, 1970). The numbers of
-, 2-, 3-, ..., digit numbers are 0, 4, 5, 6, 7, 7, 8, 9, 9, 10, 10, 10, ... (OEIS A014553; Beeler 1972; Gottlieb 1969, 1970). The numbers of 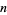 -digit numbers having maximal multiplicative persistence for
-digit numbers having maximal multiplicative persistence for 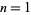 , 2, ..., are 10 (which includes the number 0), 1, 9, 12, 20, 2430, ... (OEIS A046148). The smallest
, 2, ..., are 10 (which includes the number 0), 1, 9, 12, 20, 2430, ... (OEIS A046148). The smallest 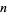 -digit numbers with maximal multiplicative persistence are 0, 77, 679, 6788, 68889, 168889, ... (OEIS A046149). The largest
-digit numbers with maximal multiplicative persistence are 0, 77, 679, 6788, 68889, 168889, ... (OEIS A046149). The largest 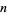 -digit numbers with maximal multiplicative persistence are 9, 77, 976, 8876, 98886, 997762, ... (OEIS A046150). The number of distinct
-digit numbers with maximal multiplicative persistence are 9, 77, 976, 8876, 98886, 997762, ... (OEIS A046150). The number of distinct 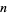 -digit numbers (except for 0s) are given by
-digit numbers (except for 0s) are given by 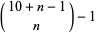 which, for
which, for 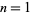 , 2, 3, ..., gives 54, 219, 714, 2001, 5004, 11439, ... (OEIS A035927).
, 2, 3, ..., gives 54, 219, 714, 2001, 5004, 11439, ... (OEIS A035927).
The concept of multiplicative persistence can be generalized to multiplying the 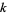 th powers of the digits of a number and iterating until the result remains constant. All numbers other than repunits, which converge to 1, converge to 0. The number of iterations required for the
th powers of the digits of a number and iterating until the result remains constant. All numbers other than repunits, which converge to 1, converge to 0. The number of iterations required for the 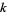 th powers of a number's digits to converge to 0 is called its
th powers of a number's digits to converge to 0 is called its 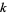 -multiplicative persistence. The following table gives the
-multiplicative persistence. The following table gives the 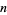 -multiplicative persistences for the first few positive integers.
-multiplicative persistences for the first few positive integers.
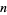 |
Sloane | 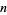 -persistences -persistences |
| 2 | A031348 | 0, 7, 6, 6, 3, 5, 5, 4, 5, 1, ... |
| 3 | A031349 | 0, 4, 5, 4, 3, 4, 4, 3, 3, 1, ... |
| 4 | A031350 | 0, 4, 3, 3, 3, 3, 2, 2, 3, 1, ... |
| 5 | A031351 | 0, 4, 4, 2, 3, 3, 2, 3, 2, 1, ... |
| 6 | A031352 | 0, 3, 3, 2, 3, 3, 3, 3, 3, 1, ... |
| 7 | A031353 | 0, 4, 3, 3, 3, 3, 3, 2, 3, 1, ... |
| 8 | A031354 | 0, 3, 3, 3, 2, 4, 2, 3, 2, 1, ... |
| 9 | A031355 | 0, 3, 3, 3, 3, 2, 2, 3, 2, 1, ... |
| 10 | A031356 | 0, 2, 2, 2, 3, 2, 3, 2, 2, 1, ... |
Erdős suggested ignoring all zeros and showed that at most 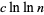 steps are needed to reduce
steps are needed to reduce 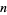 to a single digit, where
to a single digit, where 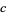 depends on the base.
depends on the base.
The smallest primes with multiplicative persistences 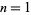 , 2, 3, ... are 2, 29, 47, 277, 769, 8867, 186889, 2678789, 26899889, 3778888999, 277777788888989, ... (OEIS A046500).
, 2, 3, ... are 2, 29, 47, 277, 769, 8867, 186889, 2678789, 26899889, 3778888999, 277777788888989, ... (OEIS A046500).
REFERENCES:
Beeler, M. Item 56 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 22, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/number.html#item56.
Carmody, P. "OEIS A003001, and a 'Zero-Length Message'." 23 Jul 2001. https://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind0107&L=NMBRTHRY&P=R1036&I=-3.
Gardner, M. Fractal Music, Hypercards, and More Mathematical Recreations from Scientific American Magazine. New York: W. H. Freeman, pp. 170 and 186, 1992.
Gottlieb, A. J. Problems 28-29 in "Bridge, Group Theory, and a Jigsaw Puzzle." Techn. Rev. 72, unpaginated, Dec. 1969.
Gottlieb, A. J. Problem 29 in "Integral Solutions, Ladders, and Pentagons." Techn. Rev. 72, unpaginated, Apr. 1970.
Guy, R. K. "The Persistence of a Number." §F25 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 262-263, 1994.
Pickover, C. A. "Persistence." Ch. 28 in Wonders of Numbers: Adventures in Mathematics, Mind, and Meaning. Oxford, England: Oxford University Press, 2001.
Rivera, C. "Problems & Puzzles: Puzzle 022-Primes & Persistence." https://www.primepuzzles.net/puzzles/puzz_022.htm.
Schneider, W. "The Persistence of a Number." https://www.wschnei.de/digit-related-numbers/persistence.html.
Sloane, N. J. A. "The Persistence of a Number." J. Recr. Math. 6, 97-98, 1973.
Sloane, N. J. A. Sequences A003001/M4687, A014553, A031346, and A046500 in "The On-Line Encyclopedia of Integer Sequences."
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 78, 1986.