

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Divisibility Tests
المؤلف:
Burton, D. M.
المصدر:
"Special Divisibility Tests." §4.3 in Elementary Number Theory, 4th ed. Boston, MA: Allyn and Bacon
الجزء والصفحة:
...
27-1-2021
1476
In general, an integer 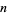 is divisible by
is divisible by 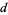 iff the digit sum
iff the digit sum 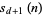 is divisible by
is divisible by 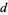 .
.
Write a positive decimal integer 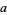 out digit by digit in the form
out digit by digit in the form 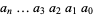 . The following rules then determine if
. The following rules then determine if 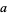 is divisible by another number by examining the congruence properties of its digits. In congruence notation,
is divisible by another number by examining the congruence properties of its digits. In congruence notation, 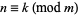 means that the remainder when
means that the remainder when 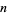 is divided by a modulus
is divided by a modulus 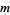 is
is 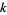 . (Note that it is always true that
. (Note that it is always true that 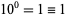 for any base.)
for any base.)
1. All integers are divisible by 1.
2. 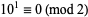 , so
, so 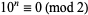 for
for 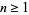 . Therefore, if the last digit
. Therefore, if the last digit 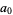 is divisible by 2 (i.e., is even), then so is
is divisible by 2 (i.e., is even), then so is 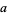 .
.
3. 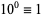 ,
, 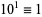 ,
, 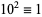 , ...,
, ..., 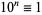 (mod 3). Therefore, if the digit sum
(mod 3). Therefore, if the digit sum 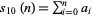 is divisible by 3, so is
is divisible by 3, so is 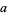 (Wells 1986, p. 48). In general, if the sum of any permutation of the digits of
(Wells 1986, p. 48). In general, if the sum of any permutation of the digits of 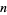 in any order is divisible by 3, then so is
in any order is divisible by 3, then so is 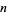 .
.
4a. 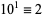 ,
, 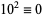 , ...,
, ..., 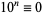 (mod 4). So if the last two digits are divisible by 4, then so is
(mod 4). So if the last two digits are divisible by 4, then so is 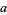 .
.
4b. If 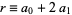 is, then so is
is, then so is 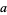 .
.
5. 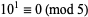 , so
, so 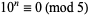 for
for 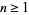 . Therefore, if the last digit
. Therefore, if the last digit 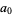 is divisible by 5 (i.e., is 5 or 0), then so is
is divisible by 5 (i.e., is 5 or 0), then so is 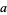 .
.
6a. If 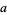 is divisible by 3 and is even, then
is divisible by 3 and is even, then 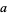 is also divisible by 6.
is also divisible by 6.
6b. 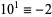 ,
, 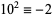 , ...,
, ..., 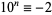 (mod 6). Therefore, if
(mod 6). Therefore, if 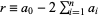 is divisible by 6, so is
is divisible by 6, so is 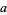 . The final number can then, of course, be further reduced using the same procedure.
. The final number can then, of course, be further reduced using the same procedure.
7a. 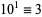 ,
, 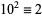 ,
, 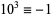 ,
, 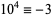 ,
, 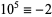 ,
, 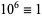 (mod 7), and the sequence then repeats. Therefore, if
(mod 7), and the sequence then repeats. Therefore, if 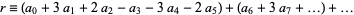 is divisible by 7, so is
is divisible by 7, so is 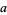 . This method was found by Pascal.
. This method was found by Pascal.
7b. An alternate test proceeds by multiplying 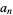 by 3 and adding to
by 3 and adding to 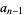 , then repeating the procedure up through
, then repeating the procedure up through 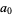 . The final number can then, of course, be further reduced using the same procedure. If the result is divisible by 7, then so is the original number (Wells 1986, p. 70).
. The final number can then, of course, be further reduced using the same procedure. If the result is divisible by 7, then so is the original number (Wells 1986, p. 70).
7c. A third test multiplies 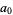 by 5 and adds it to
by 5 and adds it to 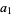 , proceeding up through
, proceeding up through 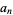 . The final number can then, of course, be further reduced using the same procedure. If the result is divisible by 7, then so is the original number (Wells 1986, p. 70).
. The final number can then, of course, be further reduced using the same procedure. If the result is divisible by 7, then so is the original number (Wells 1986, p. 70).
7d. Given a number, form two numbers  and
and 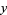 such that
such that  consists of all digits of the number except the last (units) digit and
consists of all digits of the number except the last (units) digit and 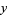 is the last digit. Compute
is the last digit. Compute 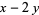 and repeat the procedure. Then the original number is divisible by 7 iff the number in the last step is divisible by 7.
and repeat the procedure. Then the original number is divisible by 7 iff the number in the last step is divisible by 7.
8. 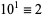 ,
, 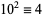 ,
, 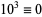 , ...,
, ..., 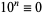 (mod 8). Therefore, if the last three digits are divisible by 8, more specifically if
(mod 8). Therefore, if the last three digits are divisible by 8, more specifically if 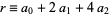 is, then so is
is, then so is 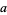 (Wells 1986, p. 72).
(Wells 1986, p. 72).
9. (Rule of nines). 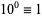 ,
, 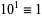 ,
, 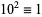 , ...,
, ..., 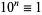 (mod 9). Therefore, if the digit sum
(mod 9). Therefore, if the digit sum 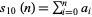 is divisible by 9, so is
is divisible by 9, so is 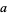 (Wells 1986, p. 74).
(Wells 1986, p. 74).
10. 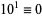 (mod 10), so if the last digit is 0, then
(mod 10), so if the last digit is 0, then 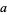 is divisible by 10.
is divisible by 10.
11. 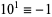 ,
, 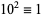 ,
, 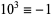 ,
, 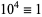 , ... (mod 11). Therefore, if
, ... (mod 11). Therefore, if 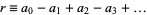 is divisible by 11, then so is
is divisible by 11, then so is 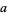 .
.
12. 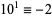 ,
, 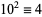 ,
, 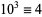 , ... (mod 12). Therefore, if
, ... (mod 12). Therefore, if 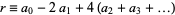 is divisible by 12, then so is
is divisible by 12, then so is 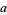 . Divisibility by 12 can also be checked by seeing if
. Divisibility by 12 can also be checked by seeing if 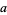 is divisible by 3 and 4.
is divisible by 3 and 4.
13. 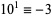 ,
, 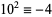 ,
, 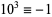 ,
, 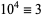 ,
, 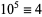 ,
, 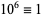 (mod 13), and the pattern repeats. Therefore, if
(mod 13), and the pattern repeats. Therefore, if 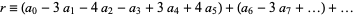 is divisible by 13, so is
is divisible by 13, so is 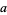 .
.
For additional tests for 13, see Gardner (1991).
An interesting piece of English language trivia is that the word "indivisibilities" has more "i"s (in fact, seven of them) than any other common word. (Other words with seven i's include, honorificabilitudinitatibus, indistinguishabilities, indivisibilities, and supercalifragilisticexpialidocious. Phrases with eight i's include "Illinois fighting Illini" and "infinite divisibility." The English word with the most possible i's is floccinaucinihilipilification (nine i's), where "floccinaucinihilipilification" means "the action or habit of estimating as worthless.")
REFERENCES:
Burton, D. M. "Special Divisibility Tests." §4.3 in Elementary Number Theory, 4th ed. Boston, MA: Allyn and Bacon, pp. 89-96, 1989.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 337-346, 2005.
Gardner, M. "Tests of Divisibility." Ch. 14 in The Unexpected Hanging and Other Mathematical Diversions. Chicago, IL: Chicago University Press, pp. 160-169, 1991.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 48, 1986.