A wide variety of large numbers crop up in mathematics. Some are contrived, but some actually arise in proofs. Often, it is possible to prove existence theorems by deriving some potentially huge upper limit which is frequently greatly reduced in subsequent versions (e.g., Graham's number, Kolmogorov-Arnold-Moser theorem, Mertens conjecture, Skewes number, Wang's conjecture).

Large decimal numbers beginning with 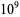 are named according to two mutually conflicting nomenclatures: the American system (in which the prefix stands for  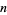in 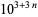) and the British system (in which the prefix stands for  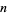in 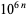). The British names for billion, trillion, etc. originate from the late 15th century when the French physician and mathematician Nicolas Chuquet (1445-1488) used the Latin prefixes to denote successive powers of one million (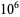) and the suffix "-llion" to refer one million (Rowlett). In more recent years, the "American" system has become widely used in England as well as in the United States (The Chicago Manual of Style 2003). This constitutes a fortunate development for standardization of terminology, albeit a somewhat regrettable development from the point of view that the British convention for representing large numbers is simpler and more logical than the American one.

The following table gives the names assigned to various powers of 10 (Woolf 1980).

American	British	power of 10
million	million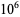
billion	milliard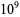
trillion	billion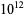
quadrillion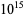
quintillion	trillion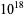
sextillion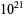
septillion	quadrillion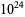
octillion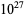
nonillion	quintillion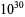
decillion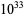
undecillion	sexillion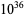
duodecillion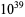
tredecillion	septillion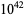
quattuordecillion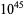
quindecillion	octillion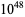
sexdecillion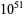
septendecillion	nonillion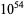
octodecillion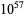
novemdecillion	decillion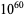
vigintillion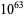
	undecillion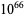
	duodecillion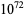
	tredecillion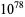
	quattuordecillion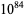
	quindecillion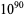
	sexdecillion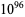
	septendecillion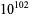
	octodecillion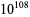
	novemdecillion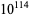
	vigintillion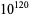
centillion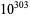
	centillion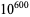

REFERENCES:

Caldwell, C. "The Largest Known Primes." https://primes.utm.edu/primes/lists/all.txt.

The Chicago Manual of Style, 15th ed. Chicago, IL: University of Chicago Press, pp. 203 and 382, 2003.

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 59-62, 1996.

Crandall, R. E. "The Challenge of Large Numbers." Sci. Amer. 276, 74-79, Feb. 1997.

Davis, P. J. The Lore of Large Numbers. New York: Random House, 1961.

Knuth, D. E. "Mathematics and Computer Science: Coping with Finiteness. Advances in Our Ability to Compute Are Bringing Us Substantially Closer to Ultimate Limitations." Science 194, 1235-1242, 1976.

Littlewood, J. E. "Newton and the Attraction of a Sphere." Math. Gaz. 32, 179-181, 1948.

Munafo, R. "Large Numbers." https://www.mrob.com/largenum.html.

Spencer, J. "Large Numbers and Unprovable Theorems." Amer. Math. Monthly 90, 669-675, 1983.

Rowlett, R. "Names for Large Numbers." https://www.ibiblio.org/units/large.html.

Woolf, H. B. (Ed. in Chief). Webster's New Collegiate Dictionary. Springfield, MA: Merriam, p. 782, 1980.