Given an expression involving known constants, integration in finite terms, computation of limits, etc., determine if the expression is equal to zero. The constant problem, sometimes also called the identity problem (Richardson 1968) is a very difficult unsolved problem in transcendental number theory. However, it is known that the problem is undecidable if the expression involves oscillatory functions such as sine. However, the Ferguson-Forcade algorithm is a practical algorithm for determining if there exist integers 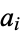 for given real numbers  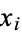such that

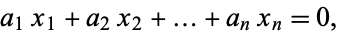or else establishing bounds within which no relation can exist (Bailey 1988).

REFERENCES:

Bailey, D. H. "Numerical Results on the Transcendence of Constants Involving 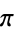, , 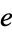and Euler's Constant." Math. Comput. 50, 275-281, 1988.

Chow, T. Y. "What is a Closed-Form Number." Amer. Math. Monthly 106, 440-448, 1999.

Chen, Z.-Z. and Kao, M.-Y. "Reducing Randomness via Irrational Numbers." 7 Jul 1999. https://arxiv.org/abs/cs.DS/9907011.

Richardson, D. "Some Unsolvable Problems Involving Elementary Functions of a Real Variable." J. Symbolic Logic 33, 514-520, 1968.

Richardson, D. "The Elementary Constant Problem." In Proc. Internat. Symp. on Symbolic and Algebraic Computation, Berkeley, July 27-29, 1992 (Ed. P. S. Wang). ACM Press, 1992.

Richardson, D. "How to Recognize Zero." J. Symb. Comp. 24, 627-645, 1997.

Sackell, J. "Zero-Equivalence in Function Fields Defined by Algebraic Differential Equations." Trans. Amer. Math. Soc. 336, 151-171, 1993.