Mirrors of Equal Curvature
المؤلف:
Walter Koechner Michael Bass
المصدر:
Solid-state Lasers
الجزء والصفحة:
158
31-1-2021
2538
Mirrors of Equal Curvature
With R1 = R2 = R we obtain, from (1),
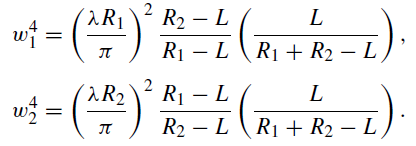............(1)
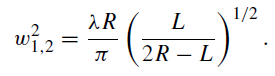......(2)
The beam waist that occurs at the center of the resonator L1 = L2 = R/2 is
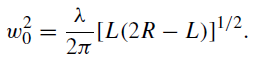.......(3)
If we further assume that the mirror radii are large compared to the resonator length R >> L, the above formula simplifies to
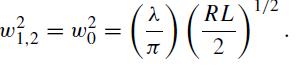..... (4)
As follows from (4) in a resonator comprised of large-radius mirrors, the beam diameter changes very little as a function of distance.
A resonator comprised of mirrors having a radius of curvature on the order of 2 to 10 m, that is, several times longer than the length of the resonator, is one of the most commonly employed configurations. Such a large-radius mirror resonator has a reasonable alignment stability and a good utilization of the active medium.
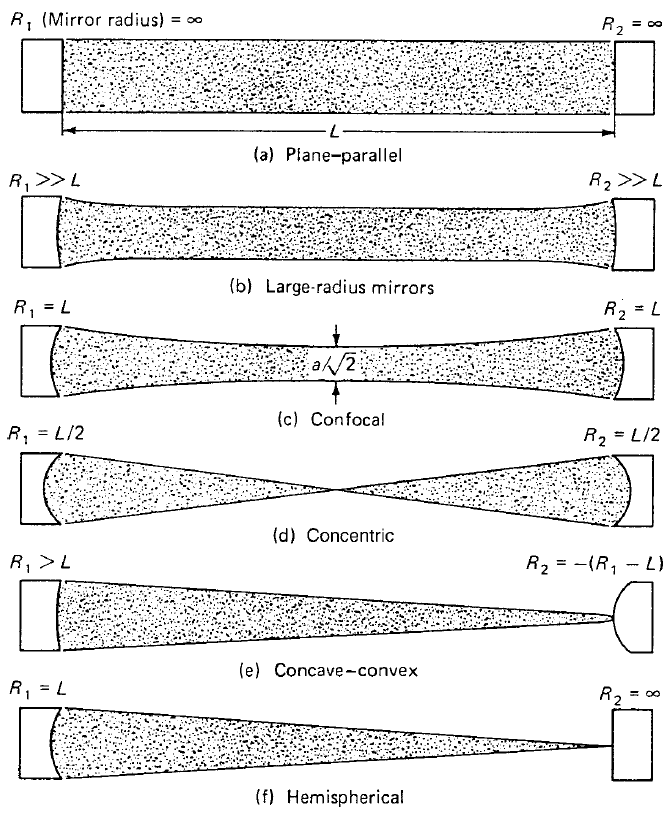
FIGURE 1. Common resonator configurations (intracavity radiation pattern is shaded).
A special case of a symmetrical configuration is the concentric resonator that consists of two mirrors separated by twice their radius, that is, R = L/2. The corresponding beam consists of a mode whose dimensions are fairly large at each mirror and which focus down to a diffraction-limited point at the center of the resonator. A concentric resonator is rather sensitive to misalignment, and the small spot can lead to optical damage.
Another very important special case of a resonator with mirrors of equal curvature is the confocal resonator. For this resonator the mirror separation equals the curvature of the identical mirrors, that is, R = L. From (2), (3) we obtain the simplified relation
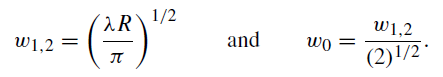.......(5)
The confocal configuration gives the smallest possible mode dimension for a resonator of given length. For this reason, confocal resonators are not often employed since they do not make efficient use of the active material.
الاكثر قراءة في مواضيع عامة في الليزر
اخر الاخبار
اخبار العتبة العباسية المقدسة
