There are at least two distinct notions of when a point process is stationary.

The most commonly utilized terminology is as follows: Intuitively, a point process 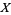 defined on a subset  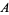of 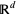 is said to be stationary if the number of points lying in  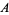depends on the size of  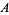but not its location. On the real line, this is expressed in terms of intervals: A point process  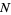on 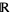 is stationary if for all  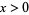and for ,

{N(t,t+x]=k} " src="https://mathworld.wolfram.com/images/equations/StationaryPointProcess/NumberedEquation1.gif" style="height:15px; width:110px" />

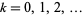depends on the length of  but not on the location .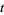

Stationary point processes of this kind were originally called simple stationary, though several authors call it crudely stationary instead. In light of the notion of crude stationarity, a different definition of stationary may be stated in which a point process 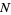 is stationary whenever for every  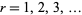and for all bounded Borel subsets  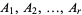of 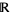, the joint distribution of {N(A_1+t),...,N(A_r+t)}" src="https://mathworld.wolfram.com/images/equations/StationaryPointProcess/Inline16.gif" style="height:15px; width:151px" /> does not depend on 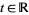. This distinction also gives rise to a related notion known as interval stationarity.

Some authors use the alternative definition of an intensity function 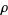, however, and conclude that a point process  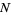is stationary whenever  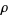is a constant function. In this case,  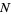may also be called homogeneous or first order stationary (Pawlas 2008).

Other notions of stationarity exist for more general spaces as well; information on such spaces can be found in the work of, e.g., Daley and Vere-Jones (2007).

REFERENCES:

Daley, D. J. and Vere-Jones, D. An Introduction to the Theory of Point Processes Volume I: Elementary Theory and Methods, 2nd ed. New York: Springer, 2003.

Daley, D. J. and Vere-Jones, D. An Introduction to the Theory of Point Processes Volume II: General Theory and Structure, 2nd ed. New York: Springer, 2007.

Pawlas, Z. "Spatial Modeling and Spatial Statistics." 2008. https://www.math.ku.dk/~pawlas/rumlig.pdf.