Let  be a rational function

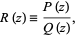(1)

where 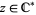,  is the Riemann sphere {infty}" src="https://mathworld.wolfram.com/images/equations/JuliaSet/Inline4.gif" style="height:15px; width:49px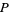" />, and  and 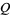 are polynomials without common divisors. The "filled-in" Julia set  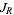is the set of points  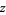which do not approach infinity after  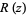is repeatedly applied (corresponding to a strange attractor). The true Julia set  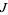is the boundary of the filled-in set (the set of "exceptional points"). There are two types of Julia sets: connected sets (Fatou set) and Cantor sets (Fatou dust).

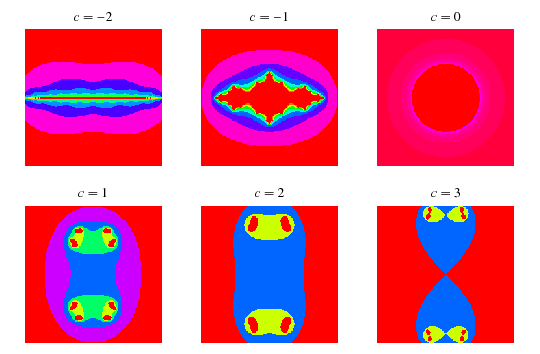
Quadratic Julia sets are generated by the quadratic mapping

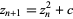(2)

for fixed 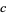. For almost every 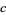, this transformation generates a fractal. Examples are shown above for various values of 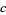. The resulting object is not a fractal for  (Dufner et al. 1998, pp. 224-226) and 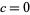 (Dufner et al. 1998, pp. 125-126), although it does not seem to be known if these two are the only such exceptional values.

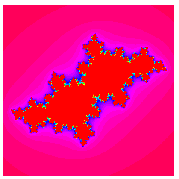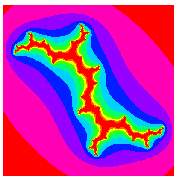
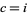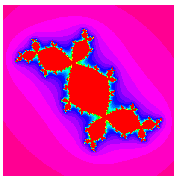
The special case of  on the boundary of the Mandelbrot set is called a dendrite fractal (top left figure), 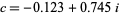 is called Douady's rabbit fractal (top right figure),  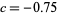is called the San Marco fractal (bottom left figure), and  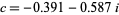is the Siegel disk fractal (bottom right figure).

The equation for the quadratic Julia set is a conformal mapping, so angles are preserved. Let 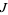 be the Julia set, then  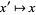leaves  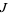invariant. If a point  is on 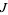, then all its iterations are on . The transformation has a two-valued inverse. If 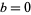 and 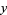 is started at 0, then the map is equivalent to the logistic map. The set of all points for which  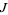is connected is known as the Mandelbrot set.

For a Julia set 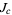 with 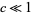, the capacity dimension is

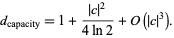(3)

For small 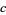,  is also a Jordan curve, although its points are not computable.

REFERENCES:

Dickau, R. M. "Julia Sets." http://mathforum.org/advanced/robertd/julias.html.

Dickau, R. M. "Another Method for Calculating Julia Sets." http://mathforum.org/advanced/robertd/inversejulia.html.

Douady, A. "Julia Sets and the Mandelbrot Set." In The Beauty of Fractals: Images of Complex Dynamical Systems (Ed. H.-O. Peitgen and D. H. Richter). Berlin: Springer-Verlag, p. 161, 1986.

Dufner, J.; Roser, A.; and Unseld, F. Fraktale und Julia-Mengen. Harri Deutsch, 1998.

Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press, pp. 124-126, 138-148, and 177-179, 1991.

Mendes-France, M. "Nevertheless." Math. Intell. 10, 35, 1988.

Peitgen, H.-O. and Saupe, D. (Eds.). "The Julia Set," "Julia Sets as Basin Boundaries," "Other Julia Sets," and "Exploring Julia Sets." §3.3.2 to 3.3.5 in The Science of Fractal Images. New York: Springer-Verlag, pp. 152-163, 1988.

Schroeder, M. Fractals, Chaos, Power Laws. New York: W. H. Freeman, p. 39, 1991.

Wagon, S. "Julia Sets." §5.4 in Mathematica in Action. New York: W. H. Freeman, pp. 163-178, 1991.

Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 126-127, 1991.