The Population Mean m and the Sample Mean x̅

Scientists find it useful to differentiate between the sample mean and the population mean. The sample mean x̅ is the arithmetic average of a limited sample drawn from a population of data. The sample mean is defined as the sum of the measurement values divided by the number of measurements as given by Equation in below.

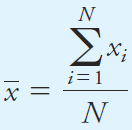
In that equation, N represents the number of measurements in the sample set. The population mean m, in contrast, is the true mean for the population. It is also defined by Equation above with the added provision that N represents the total number of measurements in the population. In the absence of systematic error, the population mean is also the true value for the measured quantity.

To emphasize the difference between the two means, the sample mean is symbolized by x̅ and the population mean by μ. More often than not, particularly when N is small, x̅ differs from m because a small sample of data may not exactly represent its population. In most cases we do not know μ and must infer its value from x̅. The probable difference between x̅ and m decreases rapidly as the number of measurements making up the sample increases; usually by the time N reaches 20 to 30, this difference is negligible. Note that the sample mean x̅ is a statistic that estimates the population parameter μ.

مواضيع ذات صلة

الشكل الوضعي للسكريات الأحادية configuration of monosaccharides

نظام استخلاص الجزئيات البسيطة

اختيار الطور الجديد وعدد مرات الاستخلاص

ميكانيكية الاستخلاص

طبيعة الصنف المستخلص

الاستخلاص بالمذيب

امتصاص الشعاع الكهرومغناطيسي وطيف الامتصاص

الطرق الكيميائية الطيفية في التحليل.

طبيعة الكيمياء التحليلية

التحليل بالحقن الجرياني المتقطع Batch flow injection analysis

الحقن الجرياني متعدد التخفيف Multi-commutation in FIA

التحليل بالحقن المتعاقب Sequential Injection Analysis