An Alternative Expression for Sample Standard Deviation

To find s with a calculator that does not have a standard deviation key, the following rearrangement is easier to use than directly applying Equation 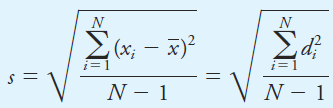1.1:

         (1.1)

Note in Example 1.1 that the difference between Σx²i and [Σxi]²/N is very small.

If we had rounded these numbers before subtracting them, a serious error would have appeared in the calculated value of s. To avoid this source of error, never round a standard deviation calculation until the very end. Furthermore, and for the same reason, never use Equation 1.2 to calculate the standard deviation of numbers containing five or more digits. Use Equation 1.1 instead. Many calculators and computers with a standard deviation function use a version of Equation 1.2 internally in the calculation. You should always be alert for roundoff errors when calculating the standard deviation of values that have five or more significant figures.

                (1.2)

When you make statistical calculations, remember that, because of the uncertainty in x, a sample standard deviation may differ significantly from the population standard deviation. As N becomes larger, x̅ and s become better estimators of m, and s.

Example 1.1

The following results were obtained in the replicate determination of the lead content of a blood sample: 0.752, 0.756, 0.752, 0.751, and 0.760 ppm Pb. Find the mean and the standard deviation of this set of data.

Solution

To apply Equation 1.2, we calculate Σx²i and (Σxi)²/N.

مواضيع ذات صلة

الشكل الوضعي للسكريات الأحادية configuration of monosaccharides

نظام استخلاص الجزئيات البسيطة

اختيار الطور الجديد وعدد مرات الاستخلاص

ميكانيكية الاستخلاص

طبيعة الصنف المستخلص

الاستخلاص بالمذيب

امتصاص الشعاع الكهرومغناطيسي وطيف الامتصاص

الطرق الكيميائية الطيفية في التحليل.

طبيعة الكيمياء التحليلية

التحليل بالحقن الجرياني المتقطع Batch flow injection analysis

الحقن الجرياني متعدد التخفيف Multi-commutation in FIA

التحليل بالحقن المتعاقب Sequential Injection Analysis