Sampling Uncertainties

Most systematic errors can be eliminated by exercising care, by calibration, and by the proper use of standards, blanks, and reference materials. Random errors, which are reflected in the precision of data, can generally be kept at an acceptable level by close control of the variables that influence the measurements. Errors due to invalid sampling are unique in the sense that they are not controllable by the use of blanks and standards or by closer control of experimental variables. For this reason, sampling errors are ordinarily treated separately from the other uncertainties associated with an analysis.

For random and independent uncertainties, the overall standard deviation so for an analytical measurement is related to the standard deviation of the sampling process ss and to the standard deviation of the method sm by the relationship

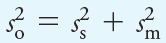       (1.1)

In many cases, the method variance will be known from replicate measurements of a single laboratory sample. Under this circumstance, s_s can be computed from measurements of s_o for a series of laboratory samples, each of which is obtained from several gross samples. An analysis of variance can reveal whether the between samples variation (sampling plus measurement variance) is significantly greater than the within samples variation (measurement variance).

Youden has shown that, once the measurement uncertainty has been reduced to one third or less of the sampling uncertainty (that is, s_m ≤ s_s/3), further improvement in the measurement uncertainty is fruitless. This result suggests that, if the sampling

uncertainty is large and cannot be improved, it is often a good idea to switch to a less precise but faster method of analysis so that more samples can be analyzed in a given length of time. Since the standard deviation of the mean is lower by a factor of √N, taking more samples can improve precision.

مواضيع ذات صلة

الشكل الوضعي للسكريات الأحادية configuration of monosaccharides

نظام استخلاص الجزئيات البسيطة

اختيار الطور الجديد وعدد مرات الاستخلاص

ميكانيكية الاستخلاص

طبيعة الصنف المستخلص

الاستخلاص بالمذيب

امتصاص الشعاع الكهرومغناطيسي وطيف الامتصاص

الطرق الكيميائية الطيفية في التحليل.

طبيعة الكيمياء التحليلية

التحليل بالحقن الجرياني المتقطع Batch flow injection analysis

الحقن الجرياني متعدد التخفيف Multi-commutation in FIA

التحليل بالحقن المتعاقب Sequential Injection Analysis