Nørlund Polynomial
المؤلف:
Gould, H. W
المصدر:
"Stirling Number Representation Problems." Proc. Amer. Math. Soc. 11
الجزء والصفحة:
...
21-9-2019
1624
Nørlund Polynomial
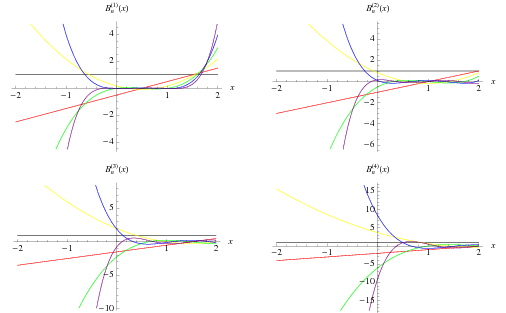
The Nørlund polynomial (note that the spelling Nörlund also appears in various publications) is a name given by Carlitz (1960) and Adelberg (1997) to the polynomial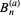 
. These are implemented in the Wolfram Language as NorlundB[n, a], and are defined through the exponential generating function
 |
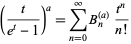(1)
|
(Carlitz 1960).
Sums involving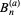 
are given by
(Carlitz 1960, Gould 1960).
The Nørlund polynomials are related to the Stirling numbers by
 |
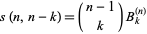(4)
|
and
 |
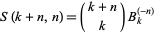(5)
|
(Carlitz 1960).
The Nørlund polynomials are a special case
 |
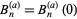(6)
|
of the function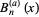 
sometimes known as the generalized Bernoulli polynomial, implemented in the Wolfram Language as NorlundB[n, a, z]. These polynomials are defined through the exponential generating function
 |
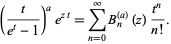(7)
|
Values of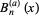 
for small positive integer 
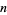and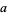 
are given by
The polynomial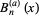 
has derivative
 |
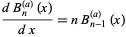(17)
|
and Maclaurin series
 |
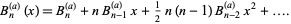(18)
|
where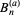 
are polynomials in 
.
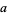REFERENCES:
Adelberg, A. "Arithmetic Properties of the Nörlund [sic] Polynomial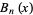 
." Oct. 28, 1997. http://citeseer.ist.psu.edu/44033.html.
Carlitz, L. "Note on Nörlund's [sic] Polynomial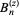 
." Proc. Amer. Math. Soc. 11, 452-455, 1960.
Gould, H. W. "Stirling Number Representation Problems." Proc. Amer. Math. Soc. 11, 447-451, 1960.
Nörlund, N. E. [sic]. Vorlesungen über Differenzenrechnung. Berlin: Springer-Verlag, 1924.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
