جزيئات ذات تناطر محوري
المؤلف:
الدكتور محمد انور بطل
المصدر:
الفيزياء الذرية والجزيئية
الجزء والصفحة:
ص 362
15-2-2022
2629
جزيئات ذات تناطر محوري
وجدنا بأن سويات الطاقة الدورانية EJK لجزيء ذو تناظر محوري وبتقريب الدائر القاسي تعطى بالعلاقة :
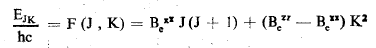
حيث F (J, K) الحد الطيفي الدوراني Bezz , Bexx ثوابت العطالة عند التوازن:
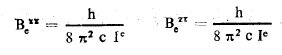
حيث ان Iexx وIezz هي على التوالي عزوم العطالة عند التوازن بالنسبة للمحور z للجزيء وبالنسبة للمحور x المتعامد مع z وهنا نميز حالتين :
a - مخروط متناظر مطاول:
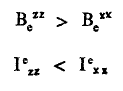
b - مخروط متناظر مسطح:
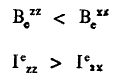
تعود هذه التسمية لطبيعة مجسم قطع الناقص للعطالة وبجسم قطع الناقص إما ذو تطور مطاول أو مسطح.
والشكلين (1) و (2) يعطيان مخططا سويات الطاقة الدورانية لجزيء، ذو تناظر محوري: وهما متعلقان في حالة المخروط المطاول والمخروط المسطح توزع سويات الطاقة بأعمدة توافق كل واحد لقيمة واحدة ل K.
ضمن كل عامود سويات الطاقة المتعاقبة توافق القيم المختلفة ل J ≥ |K| J فعندما تزداد |K| من أجل قيمة معطية ل J تنزاح سويات الطاقة نحو الأعلى (إذا كان 0 < Bezz -Bexx) أو نحو الأسفل (إذا كان 0 > Bezz -Bexx) وهذا الانزياح متناسب مع K2.
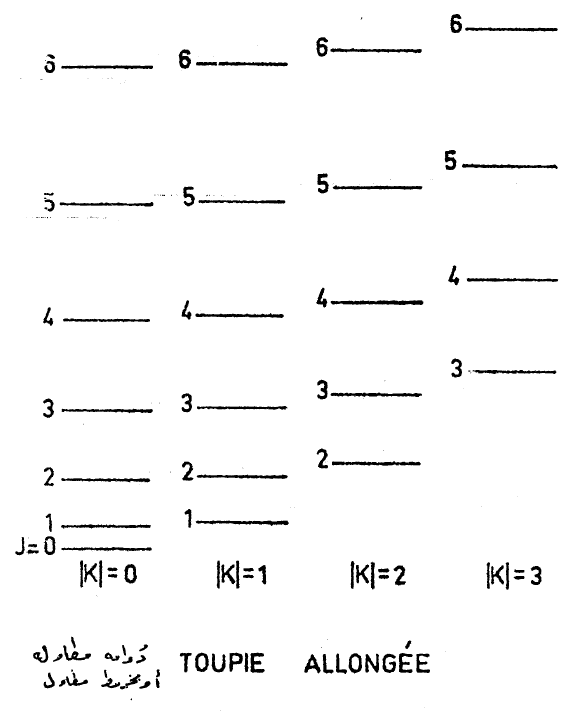
الشكل (1)
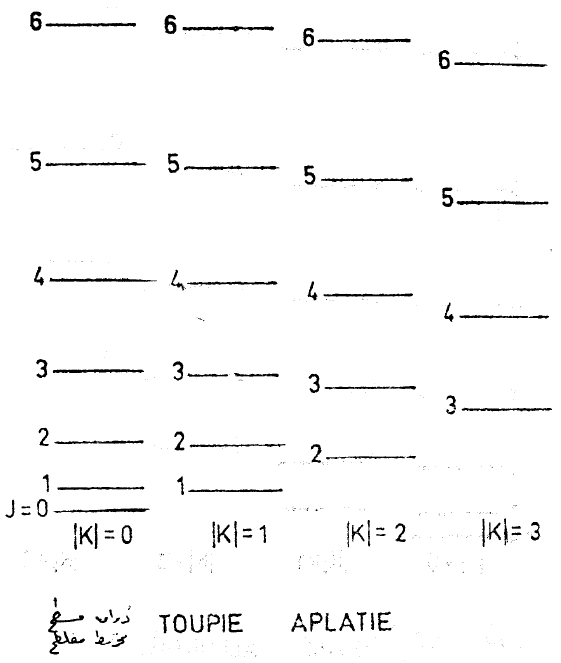
الشكل (2)
الاكثر قراءة في الفيزياء الجزيئية
اخر الاخبار
اخبار العتبة العباسية المقدسة
