تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Summation of energy
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 13
2024-02-14
1892
Now we go on to the more general consideration of what happens when there are large numbers of objects. Suppose we have the complicated problem of many objects, which we label i=1, 2, 3, …, all exerting gravitational pulls on each other. What happens then? We shall prove that if we add the kinetic energies of all the particles, and add to this the sum, over all pairs of particles, of their mutual gravitational potential energy, −GMm/rij, the total is a constant:
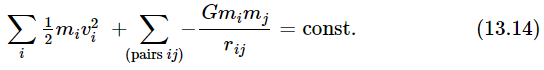
How do we prove it? We differentiate each side with respect to time and get zero. When we differentiate 1/2 mivi2, we find derivatives of the velocity that are the forces, just as in Eq. (13.5). We replace these forces by the law of force that we know from Newton’s law of gravity and then we notice that what is left is minus the time derivative of
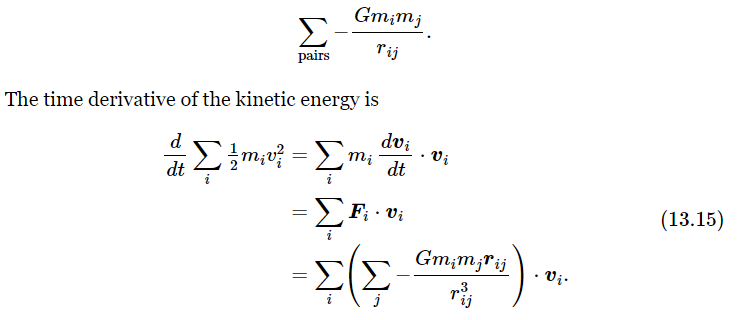

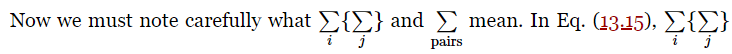
means that i takes on all values i=1, 2, 3, … in turn, and for each value of i, the index j takes on all values except i. Thus, if i=3, j takes on the values 1, 2, 4, …In Eq. (13.16), on the other hand, 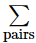 means that given values of i and j occur only once. Thus, the particle pair 1 and 3 contributes only one term to the sum. To keep track of this, we might agree to let i range over all values 1, 2, 3, …, and for each i let j range only over values greater than i. Thus, if i=3, j could only have values 4, 5, 6, … But we notice that for each i,j value there are two contributions to the sum, one involving vi, and the other vj, and that these terms have the same appearance as those of Eq. (13.15), where all values of i and j (except i=j) are included in the sum. Therefore, by matching the terms one by one, we see that Eqs. (13.16) and (13.15) are precisely the same, but of opposite sign, so that the time derivative of the kinetic plus potential energy is indeed zero. Thus, we see that, for many objects, the kinetic energy is the sum of the contributions from each individual object, and that the potential energy is also simple, it being also just a sum of contributions, the energies between all the pairs. We can understand why it should be the energy of every pair this way: Suppose that we want to find the total amount of work that must be done to bring the objects to certain distances from each other. We may do this in several steps, bringing them in from infinity where there is no force, one by one. First, we bring in number one, which requires no work, since no other objects are yet present to exert force on it. Next, we bring in number two, which does take some work, namely W12=−Gm1m2/r12. Now, and this is an important point, suppose we bring in the next object to position three. At any moment the force on number 3 can be written as the sum of two forces—the force exerted by number 1 and that exerted by number 2. Therefore, the work done is the sum of the works done by each, because if F3 can be resolved into the sum of two forces,
means that given values of i and j occur only once. Thus, the particle pair 1 and 3 contributes only one term to the sum. To keep track of this, we might agree to let i range over all values 1, 2, 3, …, and for each i let j range only over values greater than i. Thus, if i=3, j could only have values 4, 5, 6, … But we notice that for each i,j value there are two contributions to the sum, one involving vi, and the other vj, and that these terms have the same appearance as those of Eq. (13.15), where all values of i and j (except i=j) are included in the sum. Therefore, by matching the terms one by one, we see that Eqs. (13.16) and (13.15) are precisely the same, but of opposite sign, so that the time derivative of the kinetic plus potential energy is indeed zero. Thus, we see that, for many objects, the kinetic energy is the sum of the contributions from each individual object, and that the potential energy is also simple, it being also just a sum of contributions, the energies between all the pairs. We can understand why it should be the energy of every pair this way: Suppose that we want to find the total amount of work that must be done to bring the objects to certain distances from each other. We may do this in several steps, bringing them in from infinity where there is no force, one by one. First, we bring in number one, which requires no work, since no other objects are yet present to exert force on it. Next, we bring in number two, which does take some work, namely W12=−Gm1m2/r12. Now, and this is an important point, suppose we bring in the next object to position three. At any moment the force on number 3 can be written as the sum of two forces—the force exerted by number 1 and that exerted by number 2. Therefore, the work done is the sum of the works done by each, because if F3 can be resolved into the sum of two forces,
F3 = F13 + F23,
then the work is
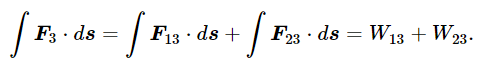
That is, the work done is the sum of the work done against the first force and the second force, as if each acted independently. Proceeding in this way, we see that the total work required to assemble the given configuration of objects is precisely the value given in Eq. (13.14) as the potential energy. It is because gravity obeys the principle of superposition of forces that we can write the potential energy as a sum over each pair of particles.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)