لم نناقش بعد قوة الاحتكاك التي يؤثّر بها سطح ما على آخر عندما يكون السطحان متحركين بالنسبة إلى بعضهما البعض. نعلم من خبرتنا أن قوة الاحتكاك تعارض الحركة النسبية. وبشكل أكثر تحديدًا، إذا كان سطحًا الجسم A والجسم B متماسين، وكان الجسم A يتحرك بسرعة 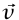 بالنسبة إلى الجسم B (شكل 2–22)، فإن قوة الاحتكاك التي يؤثر بها B على A تكون متوازية عكسيا مع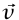. نلاحظ أيضًا أنه لكي نحافظ على السرعة النسبية ينبغي أن تكون هناك قوة أخرى مؤثّرة واحدة على الأقل. إذا كانت هذه القوة مؤثّرةً على A فلا بد أن تكون لها مركبة مسؤولة عن مطابقة قوة الاحتكاك للحفاظ على سرعة A النسبية بالنسبة إلى B من قانون نيوتن الثالث، تكون قوة الاحتكاك التي يؤثّر بها A على B متوازية مع .

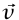يعتمد المقدار f لقوة الاحتكاك على تكوين ونعومة السطحين، وأيضًا على مقدار القوة العمودية التي يؤثّر بها أحد السطحين على الآخر. والأكثر من ذلك، قد يكون من المتوقع أيضًا أن تعتمد f على السرعة النسبية للسطحين. تجريبيا، وجد على نطاق كبير من السرعات، أن f لا تعتمد على السرعة، وأنها تتناسب طرديا مع القوة العمودية N.

وبالتالي يمكننا ذِكْر «قانون الاحتكاك الحركي» التجريبي: إذا كان سطح ما A يتحرك بسرعة بالنسبة إلى سطح B، وكان السطحان متلامسين، فإن قوة الاحتكاك التي يؤثر بها B على A تكون في اتجاه متواز عكسيًّا مع 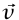، ومقدارها هو

حيث N هو مقدار القوة العمودية التي يؤثّر بها أحد السطحين على الآخر.

يُسمى المعامل μ_k معامل الاحتكاك الحركي، وهو لا يعتمد على مساحة التلامس. يجب أن يلاحظ المرء بعناية أن قانون الاحتكاك الحركي ذُكر في صورة «متساوية رياضياتية»f = μ_k N، بينما كان قانون الاحتكاك الاستاتيكي «متباينة رياضياتية» f ≤ μ_s N. عندما لا يكون هناك حركة نسبية للسطحين، فإن القوة العمودية لا تحدد منفردةً قوة الاحتكاك، أما مع وجود حركة نسبية، فإن N تحدد منفردة f. وُجد دائما لأي زوجين من الأسطح أن μ_k ≤ μ_ss. وهذه نتيجة مباشرة للإجراء التجريبي لقياس μ_s.

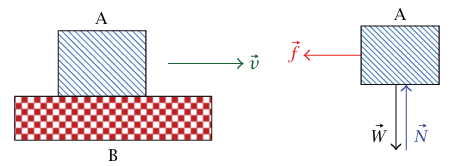
شكل 2–22: إذا كان A يتحرك نحو اليمين بالنسبة إلى B، فإن قوة الاحتكاك التي يؤثر بها B على A تكون متجهة نحو اليسار.

(افترض أن هناك كتلة وزنها W تستقر على منضدة أفقية. سوف تنزلق الكتلة إذا أثرنا بقوة أفقية 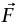 أكبر في المقدار بقدر متناهي الصغر من μ_s W. لكن بمجرد أن تكتسب الكتلة سرعة صغيرة جدًّا، فإن المنضدة ستؤثر بقوة μ_k W في اتجاه عكس الحركة. إذا كان μ_k > μ_s، فستكون هذه القوة أكبر من القوة المطبقة وستتناقص عجلة الكتلة سريعًا جدا حتى تصل إلى السكون وبالتالي، فإن وجود قوة مقدارها μ_k W سيكون ضروريا لجعل الكتلة تتحرك «بالفعل». سيبدو من وجهة نظر ميكروسكوبية في هذه الحالة، أن معامل الاحتكاك الاستاتيكي هو قيمة  μ_k وليس μ_s.)

تُعنى معظم الأمثلة المتعلقة بالاحتكاك الحركي بحالات انعدام الاتزان (تكون فيها الجسيمات متحركة بعجلة ما. رغم ذلك، إذا كانت سرعات الجسيمات ثابتةً، فلا بد أن تكون القوة على كل جسيم صفرا.

مثال 2–13 (كتلة فوق أخرى متصلتان من خلال بكرة). كتلة وزنها 100 نيوتن (N) موضوعة فوق كتلة أخرى وزنها 200 نيوتن. الكتلتان متصلتان بواسطة وتر غير قابل للمط، يمر من خلال بكرة ملساء مثبتة في حائط (شكل 2–23 (أ)). معامل الاحتكاك الحركي بين الكتلتين هو 0.6 ومعامل الاحتكاك الحركي بين الكتلة السفلية والأرضية هو 0.5. ما القوة الأفقية F التي ينبغي تطبيقها على الكتلة السفلية لإبقائها متحركةً نحو اليمين بسرعة ثابتة؟

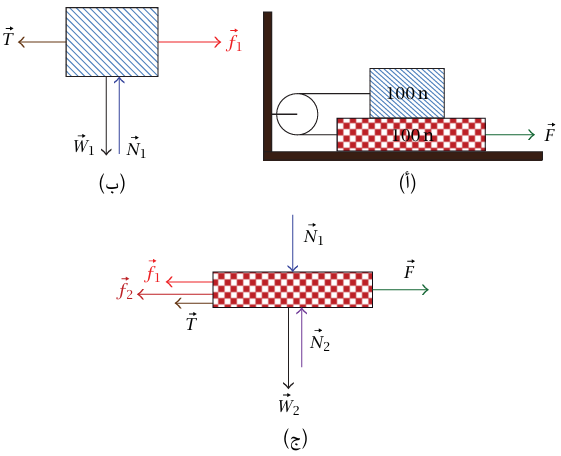
شكل 2–23 (أ) رسم توضيحي لمثال 2–13. (ب) مخطط القوى للكتلة العلوية. (ج) مخطط القوى للكتلة السفلية.

بما أن الوتر غير قابل للمط، فإن الكتلة تتحرك نحو اليسار بسرعة ثابتة (مساوية في المقدار، ومضادة في الاتجاه لسرعة الكتلة السفلية) من قانون نيوتن الأول، تكون القوة على كلٌّ من الكتلتين صفرًا. مخططا القوى للكتلتين مبينان في شكل 2–23(ب) و2–23(ج). القوى المؤثّرة على الكتلة العلوية هي:

(1) قوة الجاذبية، ومقدارها 100 نيوتن، متجهة لأسفل.

(2) القوة العمودية (مقدارها ₁N) المؤثرة بواسطة الكتلة السفلية على الكتلة العلوية ومتجهة لأعلى.

(3) القوة المؤثرة بواسطة الوتر (مقدارها T) متجهة نحو اليسار.

(4) قوة الاحتكاك (مقدارها ₁f) المؤثرة بواسطة الكتلة السفلية على الكتلة العلوية متجهة نحو اليمين.

المركبتان الرأسية والأفقية لقانون نيوتن الأول تُعطيان  n100N₁ = ، وT = f₁. علاوة على ذلك، فإن قانون الاحتكاك الحركي يُعطي f₁ = 0.6 (100 n) = 60 n؛ ومن ثُمَّ فإن T = 60 n.

القوى المؤثرة على الكتلة السفلية هي:

(1) قوة الجاذبية، ومقدارها 200 نيوتن متجهة لأسفل.

(2) القوة العمودية (مقدارها N₂) المؤثرة بواسطة الأرضية على الكتلة السفلية ومتجهة لأعلى.

(3) القوة المؤثرة بواسطة الوتر (مقدارها T) متجهة نحو اليسار.

(4) قوة الاحتكاك (مقدارها ₁f) المؤثرة بواسطة الكتلة العلوية على الكتلة السفلية، متجهة نحو اليسار.

(5) قوة الاحتكاك (مقدارها f₂) المؤثرة بواسطة الأرضية على الكتلة السفلية، متجهة نحو اليسار.

(6) القوة F متجهة نحو اليمين.

من قانون نيوتن الأول نحصل على 0 = ( n200) – N₂ – N₁ و0 = F – T – f₁ – f₂. بما أن 100 n = N₁، نجد أن 300 n = N₂. وبما أن f₂ = 0.5 N₂، نجد أن f₂ = 150 n ولأن T = 60 n وf₁ = 60 n، نجد أن F = 60 + 60 + 150 = 270 n. (إذا طُبقَتْ القوة F على الكتلة العلوية بدلًا من الكتلة السفلية، فما قيمة F المطلوبة؟ الإجابة هي أيضًا 270! نستطيع بسهولة رؤية هذا لاحقًا عند مناقشة اعتبارات الطاقة.)

بالرغم من أن المثال السابق بسيط إلى حدٍّ ما، فإن التحليل يتطلب اعتبار إحدى عشرة قوة مميزة. وهنا يُحَثُ الطالب على اكتساب عادة الترتيب بعناية (ذهنيا إن لم يكن كتابةً لكل القوى التي تعمل في أي حالة تحت الدراسة أيا كانت. دون هذا الترتيب، سيكون من المستحيل تطبيق قوانين نيوتن.