تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
استخدام قانون نيوتن الثاني لتحليل سلسلة من الأمثلة
المؤلف:
مايكل كوهين
المصدر:
الميكانيكا الكلاسيكية مقدمة أساسية
الجزء والصفحة:
ص 90 – ص 93
2024-09-12
1063
مثال 3–1 (كتلة على منحدر أملس) تنزلق كتلة m لأسفل منحدر أملس يميل على الأفقي بزاوية θ. احسب عجلة الكتلة والقوة المؤثّرة عليها بواسطة المستوى.
هناك قوتان تؤثران على الكتلة قوة تجاذبية تثاقلية مقدارها mg، متجهة رأسيًّا إلى أسفل، وقوة عمودية N يبذلها المستوى. إذا أدخلنا المحورين x وy، فإن المعادلة المتجهة 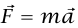 تصبح زوجا من معادلتين:
تصبح زوجا من معادلتين:

في هذه المسألة من المناسب عادةً اعتبار المحور x موازيًا للمستوى المائل، والمحور لا عموديا على المستوى المائل (شكل 1–3 (ب))؛ عندئذٍ تكون العجلة في الاتجاه x فقط، وبهذا يكون ax = a، 0 ay =. القوة العمودية ليست لها مركبة في الاتجاه x. القوة التثاقلية لها مركبة mg sin θ في الاتجاه x، ومركبة mg cos θ في الاتجاه y. بهذا تصبح المعادلة (a3–3)
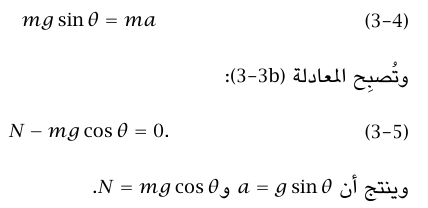
لاحظ أن قانون نيوتن الثاني لا يمكننا من حساب العجلة فقط، بل من حساب مقدار القوة العمودية N (التي حددتها حقيقة أن اتجاه العجلة معلوم بحيث يكون حاصل جمع كل القوى العمودية على ذلك الاتجاه يساوي صفرا). يعتاد العديد من الطلاب أن يكتبوا تلقائيًّا N = mg cos θ في جميع المسائل التي تحتوي على مستويات مائلة. والمثال التالي مطلوب ليبين أن N لا تساوي θ mg cos دائمًا، وأنه ليس هناك بديل عن تطبيق قوانين نيوتن بطريقة منظمة.
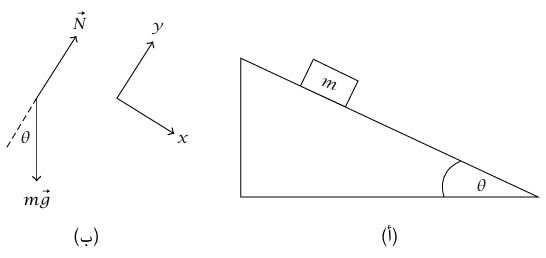
شكل 3–1: رسم توضيحي (أ) ومخطط الجسم الحر (ب) للمثال 3–1.
مثال 3–2 (كتلة على منحدر أملس متسارع). افترض أن المستوى المائل في مثال 3–1 أحد أوجه وتد (إسفين). افترض أن الوتد متسارع (متحرك بعجلة) أفقيا إلى اليمين (مثلًا، يمكن أن يكون الوتد متصلا بعربة سكة حديدية متسارعة). إذا اختيرت العجلة الصحيحة A للوتد، فإن الكتلة لن تنزلق لأعلى أو لأسفل الوتد، لكنها ستظل ساكنة بالنسبة إلى الوتد. احسب قيمة A الصحيحة، واحسب القوة التي يؤثر بها الوتد على الكتلة.
كما في المثال ،3–1، القوى الوحيدة المؤثرة على الكتلة هي قوة الجاذبية mg، متجهة لأسفل، والقوة العمودية 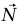 المؤثرة بواسطة الوتد. وإذا كانت الكتلة ساكنةً بالنسبة للوتد، فإنها تكون ذات عجلة
المؤثرة بواسطة الوتد. وإذا كانت الكتلة ساكنةً بالنسبة للوتد، فإنها تكون ذات عجلة 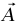 متجهة أفقيًّا إلى اليمين (لاحظ أنَّ هذه هي عجلة الكتلة بالنسبة لإطار قصوري، حالة إطار متسارع مع الوتد «غير جائزة» للاستخدام مع قانون نيوتن الثاني لأنه ليس إطارا قصوريا).
متجهة أفقيًّا إلى اليمين (لاحظ أنَّ هذه هي عجلة الكتلة بالنسبة لإطار قصوري، حالة إطار متسارع مع الوتد «غير جائزة» للاستخدام مع قانون نيوتن الثاني لأنه ليس إطارا قصوريا).
في هذه الحالة يكون من الأنسب كثيرًا اختيار المحور x أفقيا، والمحور y رأسيًا شكل (3–2). المركبتان x وy للقوة 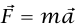 تعطيان N = mg cos θ و0 = N cos θ – mg، وبهذا نجد أن θ N = mg / cos وθ A = g tan. وحالما أخذنا المحورين x وy في اتجاه مواز وعمودي على المنحنى كما فعلنا في مثال 3–1، فإن العجلة سيكون لها مركبة x هي θ A cos، ومركبة y هي θ A sin ومن ثُمَّ فإن المركبتين x وy للقوة
تعطيان N = mg cos θ و0 = N cos θ – mg، وبهذا نجد أن θ N = mg / cos وθ A = g tan. وحالما أخذنا المحورين x وy في اتجاه مواز وعمودي على المنحنى كما فعلنا في مثال 3–1، فإن العجلة سيكون لها مركبة x هي θ A cos، ومركبة y هي θ A sin ومن ثُمَّ فإن المركبتين x وy للقوة 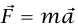 تصبحان θ mg sin θ = mA cos وθ N – mg cos θ = mA sin. بالحل لكلِّ من A وN نجد أن θ A = g tan وθ N = mg / cos، كما هو متوقع.
تصبحان θ mg sin θ = mA cos وθ N – mg cos θ = mA sin. بالحل لكلِّ من A وN نجد أن θ A = g tan وθ N = mg / cos، كما هو متوقع.
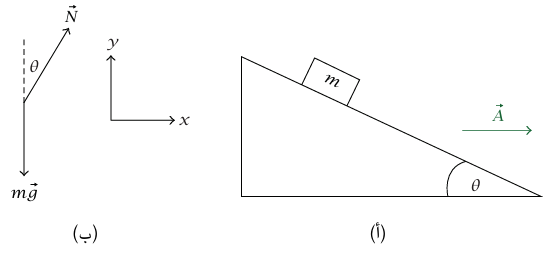
شكل 3–2: رسم توضيحي (أ) ومخطط الجسم الحر (ب) للمثال 3–2.
لاحظ بعناية أن 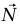 ليس لها نفس المقدار الذي في مثال 3–1. ينشأ الفرق من حقيقة أن عجلة الكتلة في مثال 3–1 موازية للمنحدر، بينما العجلة في هذا المثال أفقية.
ليس لها نفس المقدار الذي في مثال 3–1. ينشأ الفرق من حقيقة أن عجلة الكتلة في مثال 3–1 موازية للمنحدر، بينما العجلة في هذا المثال أفقية.
مثال 3–3 (امرأة في مصعد متسارع إلى أعلى). امرأة كتلتها m واقفة في مصعد متسارع. ما القوة التي تؤثّر بها الأرضية على قدميها؟
لتفادي اللَّبْس المصاحِب للإشارات، نقدِّم متجه وحدة 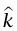 يشير رأسيا إلى أعلى. لتكن عجلة المصعد هي
يشير رأسيا إلى أعلى. لتكن عجلة المصعد هي 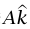 ؛ وبهذا فإن قيم A الموجبة تناظر العجلة إلى أعلى، وقيم A السالبة تناظر العجلة إلى أسفل.
؛ وبهذا فإن قيم A الموجبة تناظر العجلة إلى أعلى، وقيم A السالبة تناظر العجلة إلى أسفل.
هناك قوتان تؤثّران على المرأة (شكل 3–3): القوة التثاقلية 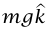 – (حيث W = mg) والقوة
– (حيث W = mg) والقوة 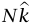 التي تبذلها الأرضية. بما أن عجلة المرأة في إطار قصوري هي
التي تبذلها الأرضية. بما أن عجلة المرأة في إطار قصوري هي 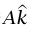 ، فإن قانون نيوتن الثاني يقضي بأن
، فإن قانون نيوتن الثاني يقضي بأن 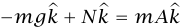 ؛ وبهذا نجد أن (g + A)N = m . إذا كانت المرأة واقفة على مقياس زنبركي، فإن مؤشر المقياس يشير إلى مقدار N. إذا كانت A موجبة (عجلة إلى أعلى)، فإن قراءة المقياس تكون أكبر من mg، و«تشعر» المرأة أنها أثقل من المعتاد. وما تشعر به فعلًا هو انضغاط العظام والغضاريف في ساقَيْها، مما يساعد قدَمَيْها على التأثير بقوة N على المقياس. إذا كانت A = – g (مصعد يسقط بحرِّية)، فإن 0 = N وتشعر المرأة بانعدام الوزن لأن قدَمَيْها لا تبذلان قوة على الأرضية. في الحقيقة، لا تزال الأرض تؤثر عليها بقوة
؛ وبهذا نجد أن (g + A)N = m . إذا كانت المرأة واقفة على مقياس زنبركي، فإن مؤشر المقياس يشير إلى مقدار N. إذا كانت A موجبة (عجلة إلى أعلى)، فإن قراءة المقياس تكون أكبر من mg، و«تشعر» المرأة أنها أثقل من المعتاد. وما تشعر به فعلًا هو انضغاط العظام والغضاريف في ساقَيْها، مما يساعد قدَمَيْها على التأثير بقوة N على المقياس. إذا كانت A = – g (مصعد يسقط بحرِّية)، فإن 0 = N وتشعر المرأة بانعدام الوزن لأن قدَمَيْها لا تبذلان قوة على الأرضية. في الحقيقة، لا تزال الأرض تؤثر عليها بقوة 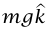 –،
–،
ولكنها تشعر بأنها كما لو كانت تعيش في فضاء خارجي لا يتعرض لأي قوى جذب تثاقلية.
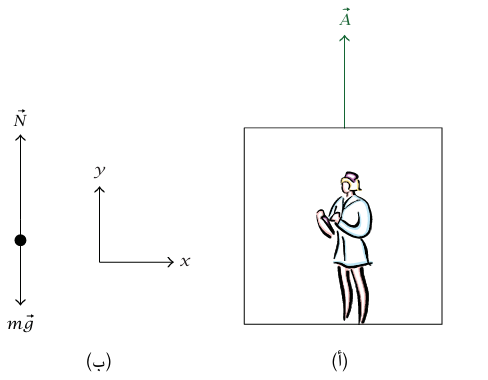
شكل 3–3: رسم توضيحي (أ) ومخطط الجسم الحر (ب) للمثال 3–3.
بصورة أعم، يمكننا إثبات أن جميع الظواهر داخل صندوق متسارع تتشابه مع الظواهر داخل صندوق غير متسارع، ولكنه على كوكب ذي عجلة جاذبية 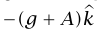 بدلًا من
بدلًا من 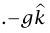 إذا لم يكن بالصندوق نوافذ تستطيع أن تنظر من خلالها إلى الخارج، فمن المستحيل أن تعلم ما إذا كان الصندوق متسارعا أم أنه ببساطة موضوع على كوكب مختلف.
إذا لم يكن بالصندوق نوافذ تستطيع أن تنظر من خلالها إلى الخارج، فمن المستحيل أن تعلم ما إذا كان الصندوق متسارعا أم أنه ببساطة موضوع على كوكب مختلف.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)