1.1 Killing vectors and Maxwell fields

Let us discuss now properties of a black hole immersed in an external magnetic field which is homogenous at infinity. We consider the magnetic field as a test field and neglect its back reaction. This problem allows an elegant solution based on the properties of Killing vector fields. We proceed as follows: a Killing vector in a vacuum spacetime generates a solution of Maxwell's equations. Let us put

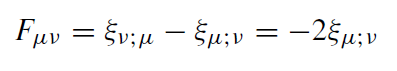 (1.1)

then

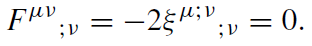 (1.2)

The commutator of two covariant derivatives turns out to be (Ricci identity)

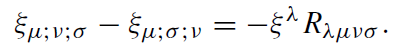 (1.3)

Permuting over the indices μ, ν, and σ, adding the resulting terms, using the Killing equation and the symmetries of the Riemann tensor, one gets

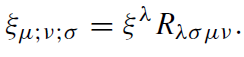 (1.4)

By contracting the indices ν and σ, we obtain

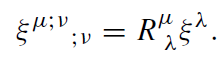 (1.5)

In a vacuum spacetime we have R^μ_λ = 0 and hence F_μν associated with the Killing vector ξ^μ satisfies the homogeneous Maxwell equation.

1.2 A black hole in a homogeneous magnetic field

The relation between the Killing vector and an electromagnetic field in Kerr geometry can be used to construct a solution describing a magnetic test field, which is homogeneous at infinity. Let us introduce two fields:

 (1.6)

At large distances F_(t)μν vanishes, while F_(φ)μν asymptotically becomes a uniform magnetic field.

It is easy to show that for any two-dimensional surface Σ surrounding a black hole

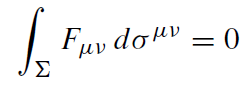 (1.7)

for both fields. Thus the magnetic monopole charge vanishes for both solutions. One also has

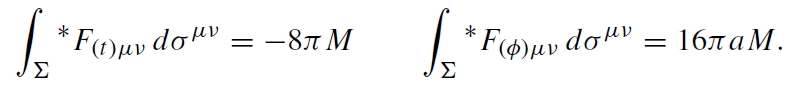 (1.8)

Here ^∗F_(t)μν = Ɛ^μναβ F_αβ. Thus, the axial Killing vector ξ_(φ) generates a stationary, axisymmetric field, which asymptotically approaches a uniform magnetic field and, moreover, has electric charge 4aM. The timelike Killing vector ξ_{(t )} generates a stationary, axisymmetric field, which vanishes at infinity and has electric charge −2M.

Combining these results we conclude that for a neutral black hole the electromagnetic field which asymptotically approaches the homogeneous magnetic field B is given by the vector potential

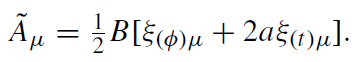 (1.9)

The electrostatic injection energy per unit charge calculated along the symmetry axis is

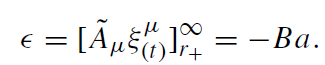 (1.10)

Carter proved that ϵ is constant over the event horizon. Thus a black hole immersed in a rarefied plasma will accrete charge until ϵ vanishes. The resulting black hole charge is

Q = 2BaM. (1.11)

The vector potential for such a black hole is

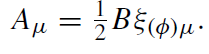 (5.12)

اخر الاخبار

اخبار العتبة العباسية المقدسة

ما الخدمات التي قدّمها موكب أشبال الطفّ لزائري عاشوراء؟

العتبة العباسية المقدسة تنظّم مسيرات عزائية لإحياء ذكرى عاشوراء في نينوى

قسم الشؤون الفكرية يحيي ذكرى استشهاد الإمام الحسين (عليه السلام) في القارة الإفريقية

قسمُ التربية والتعليم يقيم مجلسه العزائي السنوي بذكرى عاشوراء

المزيد

الآخبار الصحية

تناول الجبن.. مفيد للجسم أم خطر يهدد صحتك؟

طبيبة أسنان تحذر.. لا تتجاهل هذه العلامة بعد التنظيف

يجب أن تأكل المزيد من الشمام هذا الصيف.. إليك السبب ؟

تأثير صحي كبير.. كم بيضة يجب أن تتناول يوميا؟

المزيد

الآخبار التكنلوجية

أداء خلايا البيروفسكايت الشمسية تحت الماء قد يزيد كفاءة تحويل الكهرباء

مسافة الأمان: أساس القيادة الآمنة وتجنب الحوادث

هل القيادة السريعة تعني استهلاك اكثر للوقود؟

لماذا يعتبر كوكب المريخ غير صالح للحياة؟

المزيد

مواضيع ذات صلة

الأسرار المتبقية للثقوب السوداء ( نهاية الزمكان أم بوابة لكون آخر؟)

الثقوب الدودية

الثقوب البيضاء

الثقوب السوداء العملاقة

الثقوب السوداء

الثقوب السوداء

الطبيعة المتفردة للجاذبية

يمكن كشف التموجات الناتجة عن تصادم الثقوب السوداء في الفضاء

لماذا ندرس الثقوب السوداء؟

ماذا يحدث عند سقوط ثقب أسود في ثقب أسود؟

إطلاق النفثات

جمال التناظر