MRB Constant
المؤلف:
Burns, M. R.
المصدر:
An Alternating Series Involving n^(th) Roots." Unpublished note, 1999.
الجزء والصفحة:
...
4-3-2020
1349
MRB Constant
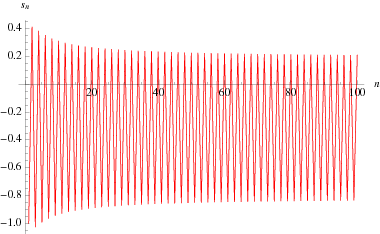
Consider the sequence of partial sums defined by
 |
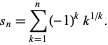(1)
|
As can be seen in the plot above, the sequence has two limit points at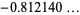 
and 0.187859... (which are separated by exactly 1). The upper limit point is sometimes known as the MRB constant after the initials of its original investigator (Burns 1999; Plouffe).
Sums for the MRB constant are given by
(Finch 2003, p. 450; OEIS A037077).
The constant can also be given as a sum over derivatives of the Dirichlet eta function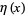 
as
where
 |
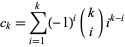(9)
|
and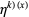 
denotes the 
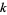th derivative of 
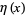evaluated at 
(Crandall 2012ab).
An integral expression for the constant is given by
![S=int_0^inftycsch(pit)I[(1+it)^(1/(1+it))]dt](http://mathworld.wolfram.com/images/equations/MRBConstant/NumberedEquation3.gif) |
(10)
|
(M. Burns, pers. comm., Jan. 21, 2020).
No closed-form expression is known for this constant (Finch 2003, p. 450).
REFERENCES:
Burns, M. R. "An Alternating Series Involving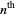 
Roots." Unpublished note, 1999.
Burns, M. R. "Try to Beat These MRB Constant Records!" http://community.wolfram.com/groups/-/m/t/366628.
Crandall, R. E. "Unified Algorithms for Polylogarithm, 
-Series, and Zeta Variants." 2012a. http://www.marvinrayburns.com/UniversalTOC25.pdf.
Crandall, R. E. "The MRB Constant." §7.5 in Algorithmic Reflections: Selected Works. PSI Press, pp. 28-29, 2012b.
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, p. 450, 2003.
Plouffe, S. "MRB Constant." http://pi.lacim.uqam.ca/piDATA/mrburns.txt.
Sloane, N. J. A. Sequences A037077 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
