Wieferich Prime
المؤلف:
Brillhart, J.; Tonascia, J.; and Winberger, P.
المصدر:
"On the Fermat Quotient." In Computers and Number Theory (Ed. A. O. L. Atkin and B. J. Birch). New York: Academic Press
الجزء والصفحة:
...
31-8-2020
920
Wieferich Prime
A Wieferich prime is a prime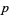 
which is a solution to the congruence equation
 |
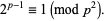(1)
|
Note the similarity of this expression to the special case of Fermat's little theorem
 |
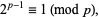(2)
|
which holds for all odd primes. The first few Wieferich primes are 1093, 3511, ... (OEIS A001220), with none other less than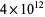 
(Lehmer 1981, Crandall 1986, Crandall et al. 1997), a limit since increased to 
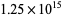(McIntosh 2004) and subsequently to 
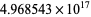by PrimeGrid as of November 2015.
Interestingly, one less than these numbers have suggestive periodic binary representations
(Johnson 1977).
If the first case of Fermat's last theorem is false for exponent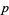 
, then 
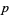must be a Wieferich prime (Wieferich 1909). If 
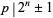with 
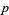and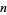 
relatively prime, then 
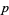is a Wieferich prime iff 
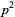also divides 
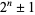. The conjecture that there are no three consecutive powerful numbers implies that there are infinitely many non-Wieferich primes (Granville 1986; Ribenboim 1996, p. 341; Vardi 1991). In addition, the abc conjecture implies that there are at least 
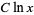non-Wieferich primes 
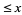for some constant 
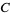(Silverman 1988, Vardi 1991).
REFERENCES:
Brillhart, J.; Tonascia, J.; and Winberger, P. "On the Fermat Quotient." In Computers and Number Theory (Ed. A. O. L. Atkin and B. J. Birch). New York: Academic Press, pp. 213-222, 1971.
Crandall, R. Projects in Scientific Computation. New York: Springer-Verlag, 1986.
Crandall, R.; Dilcher, K; and Pomerance, C. "A Search for Wieferich and Wilson Primes." Math. Comput. 66, 433-449, 1997.
Dobeš, J. "elMath.org: Project Wieferich@Home." https://elmath.org/.
Goldfeld, D. "Modular Forms, Elliptic Curves and the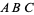 
-Conjecture." https://www.math.columbia.edu/~goldfeld/ABC-Conjecture.pdf.
Granville, A. "Powerful Numbers and Fermat's Last Theorem." C. R. Math. Rep. Acad. Sci. Canada 8, 215-218, 1986.
Guy, R. K. §A3 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, 1994.
Hardy, G. H. and Wright, E. M. Th. 91 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Johnson, W. "On the Nonvanishing of Fermat Quotients (mod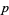 
)." J. reine angew. Math. 292, 196-200, 1977.
Lehmer, D. H. "On Fermat's Quotient, Base Two." Math. Comput. 36, 289-290, 1981.
McIntosh, R. email to Paul Zimmermann. 9 Mar 2004. https://www.loria.fr/~zimmerma/records/Wieferich.status.
Montgomery, P. "New Solutions of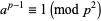 
." Math. Comput. 61, 361-363, 1991.
PrimeGrid PRPNet. "Wieferich Prime Search." https://prpnet.primegrid.com:13000.
Ribenboim, P. "Wieferich Primes." §5.3 in The New Book of Prime Number Records. New York: Springer-Verlag, pp. 333-346, 1996.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 116 and 157, 1993.
Silverman, J. "Wieferich's Criterion and the abc Conjecture." J. Number Th. 30, 226-237, 1988.
Sloane, N. J. A. Sequence A001220 in "The On-Line Encyclopedia of Integer Sequences."
Vardi, I. "Wieferich." §5.4 in Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 59-62 and 96-103, 1991.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 163, 1986.
Wieferich, A. "Zum letzten Fermat'schen Theorem." J. reine angew. Math. 136, 293-302, 1909.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
