Buffon-Laplace Needle Problem
المؤلف:
Laplace, P. S.
المصدر:
Théorie analytique des probabilités. Paris: Veuve Courcier, 1812.
الجزء والصفحة:
...
7-3-2021
2726
Buffon-Laplace Needle Problem
The Buffon-Laplace needle problem asks to find the probability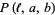 
that a needle of length 
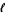will land on at least one line, given a floor with a grid of equally spaced parallel lines distances 
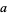and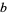 
apart, with 
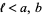. The position of the needle can be specified with points 
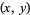and its orientation with coordinate 
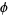. By symmetry, we can consider a single rectangle of the grid, so 
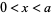and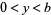 
. In addition, since opposite orientations are equivalent, we can take 
.
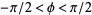The probability is given by
 |
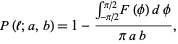(1)
|
where
 |
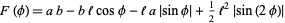(2)
|
(Uspensky 1937, p. 256; Solomon 1978, p. 4), giving
 |
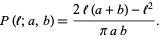(3)
|
This problem was first solved by Buffon (1777, pp. 100-104), but his derivation contained an error. A correct solution was given by Laplace (1812, pp. 359-362; Laplace 1820, pp. 365-369).
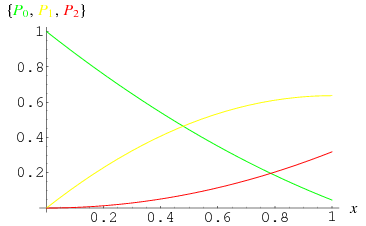
If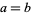 
so that 
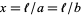and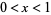 
, then the probabilities of a needle crossing 0, 1, and 2 lines are
Defining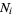 
as the number of times in 
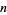tosses that a short needle crosses exactly 
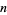lines, the variable 
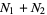has a binomial distribution with parameters 
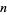and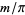 
, where 
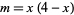(Perlman and Wichura 1975). A point estimator for 
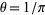is given by
 |
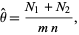(7)
|
which is a uniformly minimum variance unbiased estimator with variance
 |
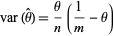(8)
|
(Perlman and Wishura 1975). An estimat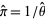or 
for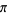 
is then given by
 |
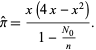(9)
|
This has asymptotic variance
 |
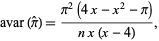(10)
|
which, for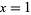 
, becomes
(OEIS A114602).
A set of sample trials is illustrated above for needles of length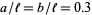 
, where needles intersecting 0 lines are shown in green, those intersecting a single line are shown in yellow, and those intersecting two lines are shown in red.
If the plane is instead tiled with congruent triangles with sides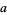 
, 
, 
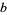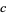, and a needle with length 
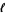less than the shortest altitude is thrown, the probability that the needle is contained entirely within one of the triangles is given by
 |
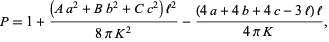(13)
|
where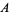 
, 
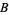, and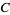 
are the angles opposite 
, 
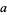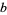, and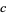 
, respectively, and 
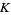is the area of the triangle. For a triangular grid consisting of equilateral triangles, this simplifies to
 |
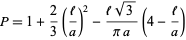(14)
|
(Markoff 1912, pp. 169-173; Uspensky 1937, p. 258).
REFERENCES:
Buffon, G. "Essai d'arithmétique morale." Histoire naturelle, générale er particulière, Supplément 4, 46-123, 1777.
Laplace, P. S. Théorie analytique des probabilités. Paris: Veuve Courcier, 1812.
Laplace, P. S. Théorie analytique des probabilités, 3rd rev. ed. Paris: Veuve Courcier, 1820.
Markoff, A. A. Wahrscheinlichkeitsrechnung. Leipzig, Germany: Teubner, 1912.
Perlman, M. and Wichura, M. "Sharpening Buffon's Needle." Amer. Stat. 20, 157-163, 1975.
Schuster, E. F. "Buffon's Needle Experiment." Amer. Math. Monthly 81, 26-29, 1974.
Sloane, N. J. A. Sequence A114602 in "The On-Line Encyclopedia of Integer Sequences."
Solomon, H. Geometric Probability. Philadelphia, PA: SIAM, pp. 3-6, 1978.
Uspensky, J. V. "Laplace's Problem." §12.17 in Introduction to Mathematical Probability. New York: McGraw-Hill, pp. 255-257, 1937.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
