Normal Distribution Function
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover,
الجزء والصفحة:
...
12-4-2021
3929
Normal Distribution Function
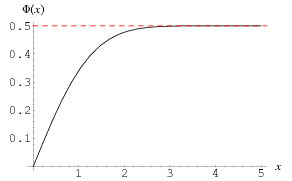
A normalized form of the cumulative normal distribution function giving the probability that a variate assumes a value in the range ![[0,x]](https://mathworld.wolfram.com/images/equations/NormalDistributionFunction/Inline1.gif)
,
 |
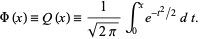(1)
|
It is related to the probability integral
 |
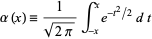(2)
|
by
 |
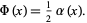(3)
|
Let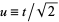 
so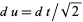 
. Then
 |
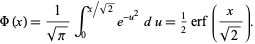(4)
|
Here, erf is a function sometimes called the error function. The probability that a normal variate assumes a value in the range ![[x_1,x_2]](https://mathworld.wolfram.com/images/equations/NormalDistributionFunction/Inline4.gif)
is therefore given by
![Phi(x_1,x_2)=1/2[erf((x_2)/(sqrt(2)))-erf((x_1)/(sqrt(2)))].](https://mathworld.wolfram.com/images/equations/NormalDistributionFunction/NumberedEquation5.gif) |
(5)
|
Neither 
nor erf can be expressed in terms of finite additions, subtractions, multiplications, and root extractions, and so must be either computed numerically or otherwise approximated.
Note that a function different from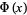 
is sometimes defined as "the" normal distribution function
(Feller 1968; Beyer 1987, p. 551), although this function is less widely encountered than the usual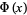 
. The notation 
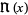is due to Feller (1971).
The value of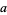 
for which 
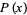falls within the interval ![[-a,a]](https://mathworld.wolfram.com/images/equations/NormalDistributionFunction/Inline23.gif)
with a given probability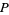 
is a related quantity called the confidence interval.
For small values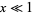 
, a good approximation to 
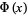is obtained from the Maclaurin series for erf,
 |
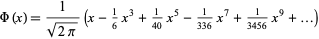(10)
|
(OEIS A014481). For large values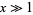 
, a good approximation is obtained from the asymptotic series for erf,
 |
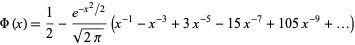(11)
|
(OEIS A001147).
The value of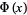 
for intermediate 
can be computed using the continued fraction identity
 |
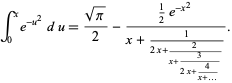(12)
|
A simple approximation of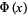 
which is good to two decimal places is given by
![Phi_1(x) approx <span style=]() {0.1x(4.4-x) for 0<=x<=2.2; 0.49 for 2.2<x<2.6; 0.50 for x>=2.6. " src="https://mathworld.wolfram.com/images/equations/NormalDistributionFunction/NumberedEquation9.gif" style="height:62px; width:247px" /> |
(13)
|
Abramowitz and Stegun (1972) and Johnson et al. (1994) give other functional approximations. An approximation due to Bagby (1995) is
![Phi_2(x)=1/2<span style=]() {1-1/(30)[7e^(-x^2/2)+16e^(-x^2(2-sqrt(2)))+(7+1/4pix^2)e^(-x^2)]}^(1/2). " src="https://mathworld.wolfram.com/images/equations/NormalDistributionFunction/NumberedEquation10.gif" style="height:34px; width:389px" /> |
(14)
|
The plots below show the differences between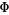 
and the two approximations.
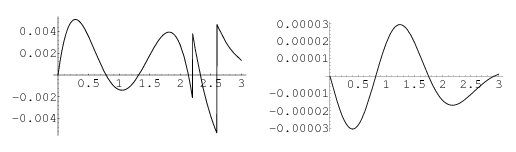
The value of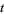 
giving 
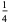is known as the probable error of a normally distributed variate.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 931-933, 1972.
Bagby, R. J. "Calculating Normal Probabilities." Amer. Math. Monthly 102, 46-49, 1995.
Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, 1987.
Bryc, W. "A Uniform Approximation to the Right Normal Tail Integral." Math. Comput. 127, 365-374, 2002.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, 1968.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 2, 3rd ed. New York: Wiley, p. 45, 1971.
Hastings, C. Approximations for Digital Computers. Princeton, NJ: Princeton University Press, 1955.
Johnson, N.; Kotz, S.; and Balakrishnan, N. Continuous Univariate Distributions, Vol. 1, 2nd ed. Boston, MA: Houghton Mifflin, 1994.
Patel, J. K. and Read, C. B. Handbook of the Normal Distribution. New York: Dekker, 1982.
Sloane, N. J. A. Sequences A001147/M3002 and A014481 in "The On-Line Encyclopedia of Integer Sequences."
Whittaker, E. T. and Robinson, G. "Normal Frequency Distribution." Ch. 8 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 164-208, 1967.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
