Compact-Open Topology
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
www.almerja.com
الجزء والصفحة:
...
31-5-2021
2677
Compact-Open Topology
The compact-open topology is a common topology used on function spaces. Suppose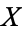 
and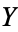 
are topological spaces and 
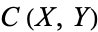is the set of continuous maps from 
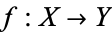. The compact-open topology on 
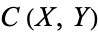is generated by subsets of the following form,
![B(K,U)=<span style=]() {f|f(K) subset U}, " src="https://mathworld.wolfram.com/images/equations/Compact-OpenTopology/NumberedEquation1.gif" style="height:18px; width:156px" /> |
(1)
|
where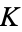 
is compact in 
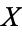and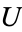 
is open in 
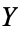. (Hence the terminology "compact-open.") It is important to note that these sets are not closed under intersection, and do not form a topological basis. Instead, the sets 
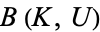form a subbasis for the compact-open topology. That is, the open sets in the compact-open topology are the arbitrary unions of finite intersections of 
.
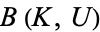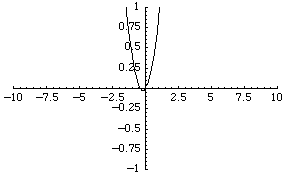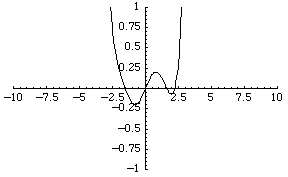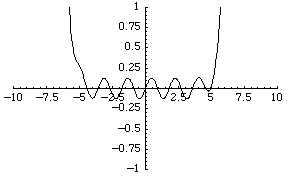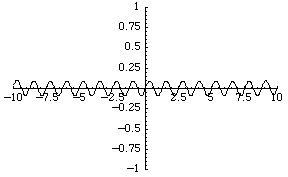
The simplest function space to compare topologies is the space of real-valued continuous functions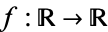 
. A sequence of functions 
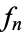converges to 
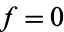iff for every 
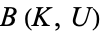containing 
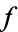contains all but a finite number of the 
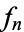. Hence, for all 
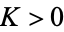and all 
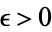, there exists an 
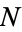such that for all 
,
 |
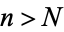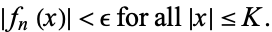(2)
|
For example, the sequence of functions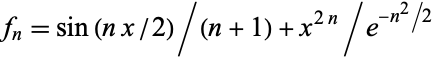 
converges to the zero function, although each function is unbounded.
When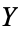 
is a metric space, the compact-open topology is the same as the topology of compact convergence. If 
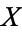is a locally compact T2-space, a fairly weak condition, then the evaluation map
 |
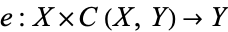(3)
|
defined by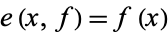 
is continuous. Similarly, 
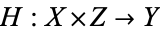is continuous iff the map 
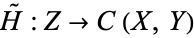, given by 
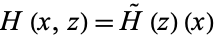, is continuous. Hence, the compact-open topology is the right topology to use in homotopy theory.
الاكثر قراءة في التبلوجيا
اخر الاخبار
اخبار العتبة العباسية المقدسة
