Hermite,s Interpolating Polynomial
المؤلف:
Bartels, R. H.; Beatty, J. C.; and Barsky, B. A
المصدر:
"Hermite and Cubic Spline Interpolation." Ch. 3 in An Introduction to Splines for Use in Computer Graphics and Geometric Modelling. San Francisco, CA: Morgan Kaufmann, pp. 9-17, 1998.
الجزء والصفحة:
...
19-11-2021
1688
Hermite's Interpolating Polynomial
Let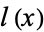 
be an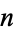 
th degree polynomial with zeros at 
, ..., 
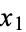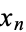. Then the fundamental Hermite interpolating polynomials of the first and second kinds are defined by
 |
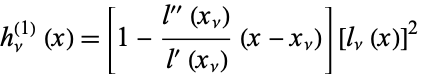(1)
|
and
![h_nu^((2))(x)=(x-x_nu)[l_nu(x)]^2](https://mathworld.wolfram.com/images/equations/HermitesInterpolatingPolynomial/NumberedEquation2.gif) |
(2)
|
for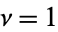 
, 2, ...
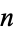, where the fundamental polynomials of Lagrange interpolation are defined by
 |
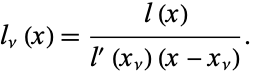(3)
|
They are denote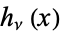d 
and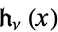 
, respectively, by Szegö (1975, p. 330).
These polynomials have the properties
for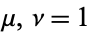 
, 2, ..., 
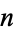. Now let 
, ..., 
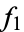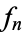and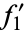 
, ..., 
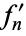be values. Then the expansion
 |
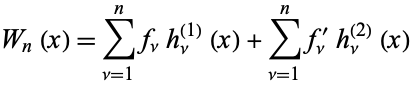(8)
|
gives the unique Hermite interpolating fundamental polynomial for which
If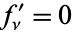 
, these are called Hermite's interpolating polynomials.
The fundamental polynomials satisfy
 |
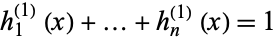(11)
|
and
 |
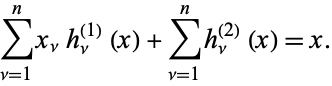(12)
|
Also, if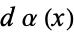 
is an arbitrary distribution on the interval ![[a,b]](https://mathworld.wolfram.com/images/equations/HermitesInterpolatingPolynomial/Inline35.gif)
, then
where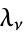 
are Christoffel numbers.
REFERENCES:
Bartels, R. H.; Beatty, J. C.; and Barsky, B. A. "Hermite and Cubic Spline Interpolation." Ch. 3 in An Introduction to Splines for Use in Computer Graphics and Geometric Modelling. San Francisco, CA: Morgan Kaufmann, pp. 9-17, 1998.
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 314-319, 1956.
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., pp. 330-332, 1975.ش
الاكثر قراءة في الرياضيات التطبيقية
اخر الاخبار
اخبار العتبة العباسية المقدسة
