The conjugate gradient method can be viewed as a special variant of the Lanczos method for positive definite symmetric systems. The minimal residual method and symmetric LQ method (SYMMLQ) are variants that can be applied to symmetric indefinite systems.

The vector sequences in the conjugate gradient method correspond to a factorization of a tridiagonal matrix similar to the coefficient matrix. Therefore, a breakdown of the algorithm can occur corresponding to a zero pivot if the matrix is indefinite. Furthermore, for indefinite matrices the minimization property of the conjugate gradient method is no longer well-defined. The MINRES and SYMMLQ methods are variants of the CG method that avoid the LU decomposition and do not suffer from breakdown. SYMMLQ solves the projected system, but does not minimize anything (it keeps the residual orthogonal to all previous ones).

When 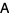 is not positive definite, but symmetric, we can still construct an orthogonal basis for the Krylov subspace by three-term recurrence relations. Eliminating the search directions in the equations of the conjugate gradient method gives a recurrence

(1)

which can be written in matrix form as

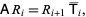(2)

where 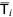 is an 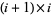 tridiagonal matrix.

In this case we have the problem that 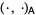 no longer defines an inner product. However we can still try to minimize the residual in the 2-norm by obtaining

(3)

that minimizes

			(4)
			(5)

Now we exploit the fact that if

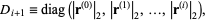(6)

then 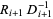 is an orthonormal transformation with respect to the current Krylov subspace:

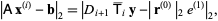(7)

and this final expression can simply be seen as a minimum norm least squares problem.

One approach is to solve the system 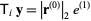, as in the conjugate gradient method ( 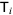is the upper  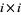part of 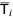). However, other than in the conjugate gradient method, we cannot rely on the existence of a Cholesky decomposition (since  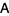is not positive definite). An alternative is then to decompose  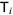by an LQ decomposition. This leads to simple recurrences and the resulting method is known as SYMMLQ (Paige and Saunders 1975).

REFERENCES:

Barrett, R.; Berry, M.; Chan, T. F.; Demmel, J.; Donato, J.; Dongarra, J.; Eijkhout, V.; Pozo, R.; Romine, C.; and van der Vorst, H. Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, 2nd ed. Philadelphia, PA: SIAM, 1994. http://www.netlib.org/linalg/html_templates/Templates.html.

Paige, C.; Parlett, B.; and van der Vorst, H. "Approximate Solutions and Eigenvalue Bounds from Krylov Subspaces." Numer. Lin. Alg. Appl. 29, 115-134, 1995.

Paige, C. and Saunders, M. "Solution of Sparse Indefinite Systems of Linear Equations." SIAM J. Numer. Anal. 12, 617-629, 1975.