Maximize the distance a Jeep can penetrate into the desert using a given quantity of fuel. The Jeep is allowed to go forward, unload some fuel, and then return to its base using the fuel remaining in its tank. At its base, it may refuel and set out again. When it reaches fuel it has previously stored, it may then use it to partially fill its tank. This problem is also called the exploration problem (Ball and Coxeter 1987).

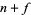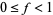Given  (with ) drums of fuel at the edge of the desert and a Jeep capable of holding one drum (and storing fuel in containers along the way), the maximum one-way distance which can be traveled (assuming the Jeep travels one unit of distance per drum of fuel expended) is

			(1)
			(2)

where 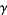 is the Euler-Mascheroni constant and  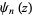the polygamma function.

For example, the farthest a Jeep with 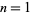 drum can travel is obviously 1 unit. However, with  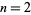drums of gas, the maximum distance is achieved by filling up the Jeep's tank with the first drum, traveling 1/3 of a unit, storing 1/3 of a drum of fuel there, and then returning to base with the remaining 1/3 of a tank. At the base, the tank is filled with the second drum. The Jeep then travels 1/3 of a unit (expending 1/3 of a drum of fuel), refills the tank using the 1/3 of a drum of fuel stored there, and continues an additional 1 unit of distance on a full tank, giving a total distance of 4/3. The solutions for 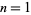, 2, ... drums are 1, 4/3, 23/15, 176/105, 563/315, ..., which can also be written as 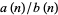, where

			(3)
			(4)

(OEIS A025550 and A025547).

REFERENCES:

Alway, G. C. "Crossing the Desert." Math. Gaz. 41, 209, 1957.

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 32, 1987.

Bellman, R. Exercises 54-55 Dynamic Programming. Princeton, NJ: Princeton University Press, p. 103, 1955.

Fine, N. J. "The Jeep Problem." Amer. Math. Monthly 54, 24-31, 1947.

Gale, D. "The Jeep Once More or Jeeper by the Dozen." Amer. Math. Monthly 77, 493-501, 1970.

Gardner, M. The Second Scientific American Book of Mathematical Puzzles & Diversions: A New Selection. New York: Simon and Schuster, pp. 152 and 157-159, 1961.

Haurath, A.; Jackson, B.; Mitchem, J.; and Schmeichel, E. "Gale's Round-Trip Jeep Problem." Amer. Math. Monthly 102, 299-309, 1995.

Havil, J. "Crossing the Desert." §13.6 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 127, 2003.

Helmer, O. "A Problem in Logistics: The Jeep Problem." Project Rand Report No. Ra 15015, Dec. 1947.

Phipps, C. G. "The Jeep Problem, A More General Solution." Amer. Math. Monthly 54, 458-462, 1947.

Sloane, N. J. A. Sequences A025550 and A025547 in "The On-Line Encyclopedia of Integer Sequences."

اخر الاخبار

اخبار العتبة العباسية المقدسة

جولة تفقدية لمتابعة خطة تنظيم مداخل المعزّين المشاركين في عزاء ركضة طويريج

لتعزيز التعاون الأكاديمي والبحثي.. جامعة الكفيل توقع اتفاقيتي توأمة مع جامعتين عراقيتين

المجمَع العلميّ يواصل إقامة مجلسه العزائي بذكرى شهادة الإمام الحسين (عليه السلام) في النجف الأشرف

قسم حفظ النظام يواصل تنفيذ خطته لتنظيم سير المواكب والزائرين في شهر المحرم

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد