محصلة المتجهات (The Resultant of the Vectors)

عند حركة جسم بين نقطتين او اكثر تتولد إزاحات متعددة لها قيمة واتجاه ولجل إيجاد المحصلة النهائية لإزاحة الجسم الكلية بين النقطة الأولى والنهائية تضاف هذه الإزاحات الى بعضها البعض او أن تطرح هذه الإزاحات من بعضها البعض (إذا كان اتجاهاتها متعاكسة) ولذلك يمكن تقسيم طريقة إيجاد محصلة الإزاحات إلى نوعين:

1-1- إضافة المتجهات (Vector Addition):

عند إضافة متجهين او اكثر إلى بعضها البعض يجب ان تكون هذه الكميات المتجهة من نفس النوع (إزاحات او قوى، مثلاً) وأن تكون ذلك وحدات قياس متماثلة، وتستخدم لأجل الإضافة طريقتان هما:

1-1-1- طريقة إكمال المثلث (Triangle  Method):

وتستخدم عادة عندما يقطع الجسم إزاحتان متعاقبتان، إحداهما تكمل الاخرى كما في الشكل رقم (1.1)، وعند ذلك يمكن تعيين محصلة الإزاحة الكلية للجسم بواسطة الرسم وذلك برسم خط مستقيم يصل بين بداية الإزاحة الاولى ونهاية الإزاحة الثانية، فيكون ذلك الخط المستقيم ممثلاً للمحصلة، كما يمكن إيجاد قيمة المحصلة رياضياً من معرفة قيمة الإزاحة الاولى والثانية ومقدار الزاوية المحصورة بينهما وذلك باستخدام قانون الجيب تمام وكما يلي:

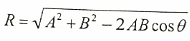
حيث R تمثل رمز المحصلة، A تمثل مقدار الإزاحة الاولى A و B تمثل مقدار الإزاحة الثانية B، و θ تمثل الزاوية المحصورة بين الإزاحتان A و B. وتكتب الصيغة الرياضية لقانون جمع الإزاحات كما يلي: R = A+B.

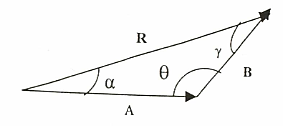
الشكل (1.1).  

اما اتجاه تلك المحصلة (أي زاوية ميلها عن المحور السيني الموجب) فيمكن إيجاده من قانون الجيب الذي يطبق على أي مثلث كما في المعادلة التالية:

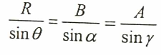
حيث الزاوية θ ، a ،B ، هي زوايا المثلث المقابلة للأضلاع R،B،A على التوالي، فإذا علم أي ثلاث مقادير من النسب المثلثية السابقة يمكن إيجاد المقدار الرابع.

2-1-1- طريقة إكمال متوازي أضلاع (Parallelogram Method):

تستخدم هذه الطريقة عندما تنطلق الإزاحتان من نقطة واحدة كما في الشكل رقم (2.1). ولتعيين الإزاحة المحصلة على الرسم يتم إكمال شكل متوازي أضلاع وذلك برسم مستقيم مساوي وموازي للإزاحة الاولى من نقطة نهاية الإزاحة الثانية ومستقيم أخر مساوي وموازي للإزاحة الثانية من نقطة نهاية الإزاحة الأولى وبذلك فإن الإزاحة المحصلة سوف تمثل قطر متوازي الأضلاع الذي يمر بنقطة بداية الحركة، حيث يمكن وضع معادلة متجه المحصلة كما يلي:

R = A+B 

ويمكن حساب قيمة محصلة الإزاحة من قانون الجيب تمام السابق مع تغيير بسيط في إشارة الحد الثالث لتصبح موجبة وكما يلي:

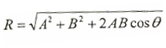
حيث θ هي الزاوية المحصورة بين المتجهين.

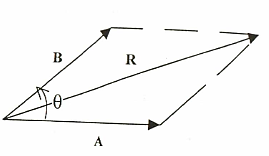
الشكل (2.1)

ومن المفيد ذكر بعض المواصفات المهمة للتعامل مع المتجهات:

1- ان محصلة متجهين لا تعتمد على ترتيب جمعها (أي أن عملية الجمع تبادلية) حيث يمكن القول أن :

 R = A+B = B+A

2- عدد إيجاد محصلة ثلاث متجهات او أكثر كما في الشكل رقم (3.1) يجب اختيار أي متجهين متجاورين لإيجاد محصلتهما اولاً ثم معاملة تلك المحصلة مع المتجه الثالث القريب لإيجاد المحصلة الثانية او النهائية، ولا يعتمد ذلك على تسلسل معاملة المتجهات مع بعضها البعض حيث يمكن القول أن:

R = A+ (B+C) = (A+B)+C

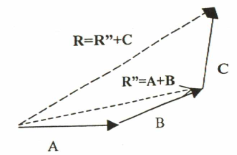
 الشكل (3.1)

2-1- طرح المتجهات (Subtraction of Vectors):

وتستخدم هذه الطريقة لإيجاد محصلة إزاحتان او اكثر عند تعاكس إحداها الاخرى في الاتجاه أو كلياً. ويمكن الاستفادة من مفهوم المتجه السالب (The Neghative of a Vector) لتغيير عملية طرح المتجهات إلى عملية جمع ثم التعامل معها. ويعرف المتجه السالب على أنه المتجه الذي إذا أضيف إلى المتجه الأصلي ستكون محصلة جمع المتجهين صفراً. فمثلاً إذا أضيف المتجه السالب (-A) إلى المتجه A كانت محصلة جمع المتجهين ستكون صفراً حيث المتجه –A يساوي بالقيمة المتجه A وبعاكسه بالاتجاه وكما يلي:

 A+ (-A) = 0

واستناداً إلى هذا المفهوم يمكن تحويل عملية طرح أي متجهين إلى عملية جميع بأخذ المتجه السالب للثاني وكما يلي:

A-B = A+(-B)

ويمثل الشكل رقم (4.1) عملية طرح متجهين حيث يلاحظ أن المتجه B يعاكس جزئياً اتجاه حركة المتجه A، وهذا يحصل إذا زادت الزاوية المحصورة بين المتجهين المتعاقبين عن 90^o، وبذلك يمكن رسم المتجه –B بالاتجاه المعاكس للمتجه B على ان يكون مساوياً له بالمقدار حيث عندئذ فقط يمكن معاملة المتجه A مع المتجه B- على أنها عملية جمع متجهين. ولإيجاد قيمة محصلة الحركة R، يجب معرفة الزاوية θ المحصورة بين المتجه A والمتجه –B ثم نستخدم قانون جيب التمام:

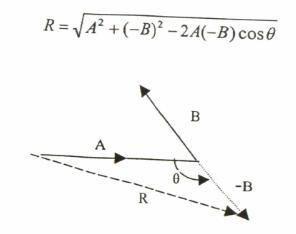
 الشكل (4.1)

ومن الميزات المهمة الاخرى للمتجهات أنها إذا ضربت بكمية غير متجهة (عديدة) فإن الناتج عبارة عن متجه جديد قيمته تساوي حاصل ضرب قيمة المتجه في قيمة الكمية العددية واتجاهه سوف يكون باتجاه الأولي، وكمثال على ذلك إذا ضرب المتجه A بالكمية غير المتجهة m فإن الناتج يساوي: