تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Relativistic mass
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 16
2024-02-27
2103
We learned in the last chapter that the mass of an object increases with velocity, but no demonstration of this was given, in the sense that we made no arguments analogous to those about the way clocks have to behave. However, we can show that, as a consequence of relativity plus a few other reasonable assumptions, the mass must vary in this way. (We have to say “a few other assumptions” because we cannot prove anything unless we have some laws which we assume to be true, if we expect to make meaningful deductions.) To avoid the need to study the transformation laws of force, we shall analyze a collision, where we need know nothing about the laws of force, except that we shall assume the conservation of momentum and energy. Also, we shall assume that the momentum of a particle which is moving is a vector and is always directed in the direction of the velocity. However, we shall not assume that the momentum is a constant times the velocity, as Newton did, but only that it is some function of velocity. We thus write the momentum vector as a certain coefficient times the vector velocity:

We put a subscript v on the coefficient to remind us that it is a function of velocity, and we shall agree to call this coefficient mv the “mass.” Of course, when the velocity is small, it is the same mass that we would measure in the slow-moving experiments that we are used to. Now we shall try to demonstrate that the formula for mv must be 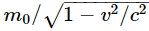 , by arguing from the principle of relativity that the laws of physics must be the same in every coordinate system.
, by arguing from the principle of relativity that the laws of physics must be the same in every coordinate system.
Suppose that we have two particles, like two protons, that are absolutely equal, and they are moving toward each other with exactly equal velocities. Their total momentum is zero. Now what can happen? After the collision, their directions of motion must be exactly opposite to each other, because if they are not exactly opposite, there will be a nonzero total vector momentum, and momentum would not have been conserved. Also, they must have the same speeds, since they are exactly similar objects; in fact, they must have the same speed they started with, since we suppose that the energy is conserved in these collisions. So, the diagram of an elastic collision, a reversible collision, will look like Fig. 16–2(a): all the arrows are the same length, all the speeds are equal. We shall suppose that such collisions can always be arranged, that any angle θ can occur, and that any speed could be used in such a collision. Next, we notice that this same collision can be viewed differently by turning the axes, and just for convenience we shall turn the axes, so that the horizontal splits it evenly, as in Fig. 16–2(b). It is the same collision redrawn, only with the axes turned.
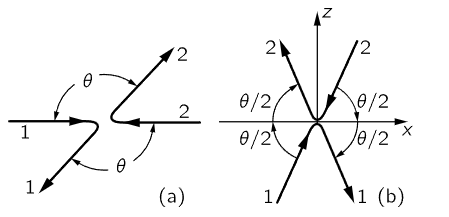
Fig. 16–2. Two views of an elastic collision between equal objects moving at the same speed in opposite directions.
Now here is the real trick: let us look at this collision from the point of view of someone riding along in a car that is moving with a speed equal to the horizontal component of the velocity of one particle. Then how does the collision look? It looks as though particle 1 is just going straight up, because it has lost its horizontal component, and it comes straight down again, also because it does not have that component. That is, the collision appears as shown in Fig. 16–3(a). Particle 2, however, was going the other way, and as we ride past it appears to fly by at some terrific speed and at a smaller angle, but we can appreciate that the angles before and after the collision are the same. Let us denote by u the horizontal component of the velocity of particle 2, and by w the vertical velocity of particle 1.
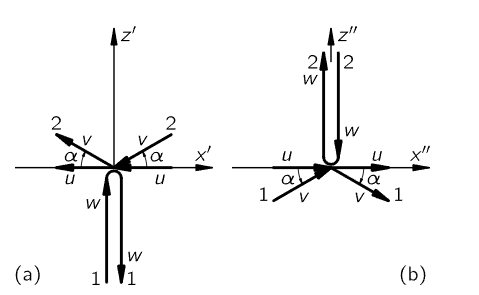
Fig. 16–3. Two more views of the collision, from moving cars.
Now the question is, what is the vertical velocity u tan α? If we knew that, we could get the correct expression for the momentum, using the law of conservation of momentum in the vertical direction. Clearly, the horizontal component of the momentum is conserved: it is the same before and after the collision for both particles, and is zero for particle 1. So, we need to use the conservation law only for the upward velocity u tan α. But we can get the upward velocity, simply by looking at the same collision going the other way! If we look at the collision of Fig. 16–3(a) from a car moving to the left with speed u, we see the same collision, except “turned over,” as shown in Fig. 16–3(b). Now particle 2 is the one that goes up and down with speed w, and particle 1 has picked up the horizontal speed u. Of course, now we know what the velocity u tan α is: it is 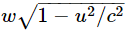 (see Eq. 16.7). We know that the change in the vertical momentum of the vertically moving particle is
(see Eq. 16.7). We know that the change in the vertical momentum of the vertically moving particle is
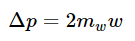
(2, because it moves up and back down). The obliquely moving particle has a certain velocity v whose components we have found to be u and 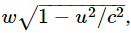 and whose mass is mv. The change in vertical momentum of this particle is therefore
and whose mass is mv. The change in vertical momentum of this particle is therefore 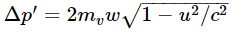 because, in accordance with our assumed law (16.8), the momentum component is always the mass corresponding to the magnitude of the velocity times the component of the velocity in the direction of interest. Thus, in order for the total momentum to be zero the vertical momenta must cancel and the ratio of the mass moving with speed v and the mass moving with speed w must therefore be
because, in accordance with our assumed law (16.8), the momentum component is always the mass corresponding to the magnitude of the velocity times the component of the velocity in the direction of interest. Thus, in order for the total momentum to be zero the vertical momenta must cancel and the ratio of the mass moving with speed v and the mass moving with speed w must therefore be

Let us take the limiting case that w is infinitesimal. If w is very tiny indeed, it is clear that v and u are practically equal. In this case, mw→m0 and mv→mu. The grand result is

It is an interesting exercise now to check whether or not Eq. (16.9) is indeed true for arbitrary values of w, assuming that Eq. (16.10) is the right formula for the mass. Note that the velocity v needed in Eq. (16.9) can be calculated from the right-angle triangle:
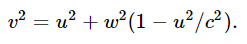
It will be found to check out automatically, although we used it only in the limit of small w.
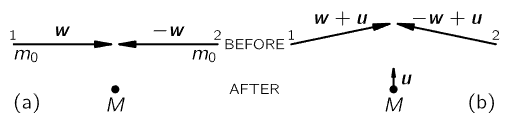
Fig. 16–4. Two views of an inelastic collision between equally massive objects.
Now, let us accept that momentum is conserved and that the mass depends upon the velocity according to (16.10) and go on to find what else we can conclude. Let us consider what is commonly called an inelastic collision. For simplicity, we shall suppose that two objects of the same kind, moving oppositely with equal speeds w, hit each other and stick together, to become some new, stationary object, as shown in Fig. 16–4(a). The mass m of each corresponds to w, which, as we know, is 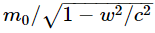 . If we assume the conservation of momentum and the principle of relativity, we can demonstrate an interesting fact about the mass of the new object which has been formed. We imagine an infinitesimal velocity u at right angles to w (we can do the same with finite values of u, but it is easier to understand with an infinitesimal velocity), then look at this same collision as we ride by in an elevator at the velocity −u. What we see is shown in Fig. 16–4(b). The composite object has an unknown mass M. Now object 1 moves with an upward component of velocity u and a horizontal component which is practically equal to w, and so also does object 2. After the collision we have the mass M moving upward with velocity u, considered very small compared with the speed of light, and also small compared with w. Momentum must be conserved, so let us estimate the momentum in the upward direction before and after the collision. Before the collision we have p≈2mwu, and after the collision the momentum is evidently p′=Muu, but Mu is essentially the same as M0 because u is so small. These momenta must be equal because of the conservation of momentum, and therefore
. If we assume the conservation of momentum and the principle of relativity, we can demonstrate an interesting fact about the mass of the new object which has been formed. We imagine an infinitesimal velocity u at right angles to w (we can do the same with finite values of u, but it is easier to understand with an infinitesimal velocity), then look at this same collision as we ride by in an elevator at the velocity −u. What we see is shown in Fig. 16–4(b). The composite object has an unknown mass M. Now object 1 moves with an upward component of velocity u and a horizontal component which is practically equal to w, and so also does object 2. After the collision we have the mass M moving upward with velocity u, considered very small compared with the speed of light, and also small compared with w. Momentum must be conserved, so let us estimate the momentum in the upward direction before and after the collision. Before the collision we have p≈2mwu, and after the collision the momentum is evidently p′=Muu, but Mu is essentially the same as M0 because u is so small. These momenta must be equal because of the conservation of momentum, and therefore

The mass of the object which is formed when two equal objects collide must be twice the mass of the objects which come together. You might say, “Yes, of course, that is the conservation of mass.” But not “Yes, of course,” so easily, because these masses have been enhanced over the masses that they would be if they were standing still, yet they still contribute, to the total M, not the mass they have when standing still, but more. Astonishing as that may seem, in order for the conservation of momentum to work when two objects come together, the mass that they form must be greater than the rest masses of the objects, even though the objects are at rest after the collision!
 الاكثر قراءة في النظرية النسبية الخاصة
الاكثر قراءة في النظرية النسبية الخاصة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)