


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 12-12-2016
التاريخ: 31-8-2019
التاريخ: 2023-05-29
التاريخ: 5-7-2016
|
مركبات المتجهات (Component of the Vector)
لقد عرفنا مما سبق أنه يمكن تعريف أن كمية متجهة بمعرفة قيمة واتجاه تلك الكمية، وبنفس الوقت يمكن تمثيل المتجه بدلالة ما يسمى بمركبات الكمية المتجهة حيث تكون المركبة الاولى باتجاه المحور السيني، وتسمى بالمركبة السينية، والمركبة الثانية باتجاه المحور الصادي، وتسمى بالمركبة الصادية، وبذلك يمكن وضع معادلة المتجه (A) على النحو التالي:
A = Ax + Ay
حيث Ax تمثل المركبة على المحور السيني، Ay تمثل المركبة على المحور الصادي، وحيث أن المركبتان متعامدتان ، كما يتضح من الشكل (1.1) فإنهما تتواقفان مع نظرية فيثاغورس حيث يمكن القول أن : A2 = A2x + A2y
ويمكن إيجاد قيمة مركبات المتجه على المحورين إذا علمنا قيمة المتجه وزاوية ميله عند الأفق حيث:
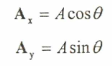
كما يمكن معرفة زاوية ميل المتجه (A) إذا علم مقدار مركباته على المحورين، السيني والصادي، حيث:
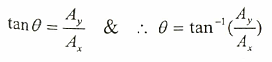
ويمكن القول أن مركبة المتجه موجية الإشارة إذا كانت باتجاه المحور السيني الموجب أو المحور الصادي الموجب، وتكون سالبة الإشارة إذا اتجهت باتجاه المحور السيني أو الصادي السالب.
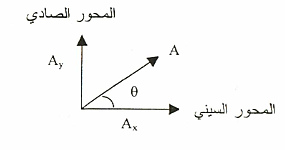
الشكل (1.1) يبين تحليل المتجه إلى مركباته



|
|
|
|
مقاومة الأنسولين.. أعراض خفية ومضاعفات خطيرة
|
|
|
|
|
|
|
أمل جديد في علاج ألزهايمر.. اكتشاف إنزيم جديد يساهم في التدهور المعرفي ؟
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقيم ندوة علمية عن روايات كتاب نهج البلاغة
|
|
|