Now we go to the cone vision, to the brighter vision, and we come to the question which is most characteristic of cone vision, and that is color. As we know, white light can be split by a prism into a whole spectrum of wavelengths which appear to us to have different colors; that is what colors are, of course: appearances. Any source of light can be analyzed by a grating or a prism, and one can determine the spectral distribution, i.e., the “amount” of each wavelength. A certain light may have a lot of blue, considerable red, very little yellow, and so on. That is all very precise in the sense of physics, but the question is, what color will it appear to be? It is evident that the different colors depend somehow upon the spectral distribution of the light, but the problem is to find what characteristics of the spectral distribution produce the various sensations. For example, what do we have to do to get a green color? We all know that we can simply take a piece of the spectrum which is green. But is that the only way to get green, or orange, or any other color?

Is there more than one spectral distribution which produces the same apparent visual effect? The answer is, definitely yes. There is a very limited number of visual effects, in fact just a three-dimensional manifold of them, as we shall shortly see, but there is an infinite number of different curves that we can draw for the light that comes from different sources. Now the question we have to discuss is, under what conditions do different distributions of light appear as exactly the same color to the eye?

The most powerful psycho-physical technique in color judgment is to use the eye as a null instrument. That is, we do not try to define what constitutes a green sensation, or to measure in what circumstances we get a green sensation, because it turns out that this is extremely complicated. Instead, we study the conditions under which two stimuli are indistinguishable. Then we do not have to decide whether two people see the same sensation in different circumstances, but only whether, if for one person two sensations are the same, they are also the same for another. We do not have to decide whether, when one sees something green, what it feels like inside is the same as what it feels like inside someone else when he sees something green; we do not know anything about that.

To illustrate the possibilities, we may use a series of four projector lamps which have filters on them, and whose brightnesses are continuously adjustable over a wide range: one has a red filter and makes a spot of red light on the screen, the next one has a green filter and makes a green spot, the third one has a blue filter, and the fourth one is a white circle with a black spot in the middle of it. Now if we turn on some red light, and next to it put some green, we see that in the area of overlap it produces a sensation which is not what we call reddish green, but a new color, yellow in this particular case. By changing the proportions of the red and the green, we can go through various shades of orange and so forth. If we have set it for a certain yellow, we can also obtain that same yellow, not by mixing these two colors but by mixing some other ones, perhaps a yellow filter with white light, or something like that, to get the same sensation. In other words, it is possible to make various colors in more than one way by mixing the lights from various filters.

What we have just discovered may be expressed analytically as follows. A particular yellow, for example, can be represented by a certain symbol Y, which is the “sum” of certain amounts of red-filtered light (R) and green-filtered light (G). By using two numbers, say r and g, to describe how bright the R and G are, we can write a formula for this yellow:

The question is, can we make all the different colors by adding together two or three lights of different, fixed colors? Let us see what can be done in that connection. We certainly cannot get all the different colors by mixing only red and green, because, for instance, blue never appears in such a mixture. However, by putting in some blue the central region, where all three spots overlap, may be made to appear to be a fairly nice white. By mixing the various colors and looking at this central region, we find that we can get a considerable range of colors in that region by changing the proportions, and so it is not impossible that all the colors can be made by mixing these three colored lights. We shall discuss to what extent this is true; it is in fact essentially correct, and we shall shortly see how to define the proposition better.

In order to illustrate our point, we move the spots on the screen so that they all fall on top of each other, and then we try to match a particular color which appears in the annular ring made by the fourth lamp. What we once thought was “white” coming from the fourth lamp now appears yellowish. We may try to match that by adjusting the red and green and blue as best we can by a kind of trial and error, and we find that we can approach rather closely this particular shade of “cream” color. So, it is not hard to believe that we can make all colors. We shall try to make yellow in a moment, but before we do that, there is one color that might be very hard to make. People who give lectures on color make all the “bright” colors, but they never make brown, and it is hard to recall ever having seen brown light. As a matter of fact, this color is never used for any stage effect, one never sees a spotlight with brown light; so we think it might be impossible to make brown. In order to find out whether it is possible to make brown, we point out that brown light is merely something that we are not used to seeing without its background. As a matter of fact, we can make it by mixing some red and yellow. To prove that we are looking at brown light, we merely increase the brightness of the annular background against which we see the very same light, and we see that that is, in fact, what we call brown! Brown is always a dark color next to a lighter background. We can easily change the character of the brown. For example, if we take some green out we get a reddish brown, apparently a chocolaty reddish brown, and if we put more green into it, in proportion, we get that horrible color which all the uniforms of the Army are made of, but the light from that color is not so horrible by itself; it is of yellowish green, but seen against a light background.

Now we put a yellow filter in front of the fourth light and try to match that. (The intensity must of course be within the range of the various lamps; we cannot match something which is too bright, because we do not have enough power in the lamp.) But we can match the yellow; we use a green and red mixture, and put in a touch of blue to make it even more perfect. Perhaps we are ready to believe that, under good conditions, we can make a perfect match of any given color.

Now let us discuss the laws of color mixture. In the first place, we found that different spectral distributions can produce the same color; next, we saw that “any” color can be made by adding together three special colors, red, blue, and green. The most interesting feature of color mixing is this: if we have a certain light, which we may call X, and if it appears indistinguishable from Y, to the eye (it may be a different spectral distribution, but it appears indistinguishable), we call these colors “equal,” in the sense that the eye sees them as equal, and we write

Here is one of the great laws of color: if two spectral distributions are indistinguishable, and we add to each one a certain light, say Z (if we write X+Z, this means that we shine both lights on the same patch), and then we take Y and add the same amount of the same other light, Z, the new mixtures are also indistinguishable:

We have just matched our yellow; if we now shine pink light on the whole thing, it will still match. So, adding any other light to the matched lights leaves a match. In other words, we can summarize all these color phenomena by saying that once we have a match between two colored lights, seen next to each other in the same circumstances, then this match will remain, and one light can be substituted for the other light in any other color mixing situation. In fact, it turns out, and it is very important and interesting, that this matching of the color of lights is not dependent upon the characteristics of the eye at the moment of observation: we know that if we look for a long time at a bright red surface, or a bright red light, and then look at a white paper, it looks greenish, and other colors are also distorted by our having looked so long at the bright red. If we now have a match between, say, two yellows, and we look at them and make them match, then we look at a bright red surface for a long time, and then turn back to the yellow, it may not look yellow any more; I do not know what color it will look, but it will not look yellow. Nevertheless the yellows will still look matched, and so, as the eye adapts to various levels of intensity, the color match still works, with the obvious exception of when we go into the region where the intensity of the light gets so low that we have shifted from cones to rods; then the color match is no longer a color match, because we are using a different system.

The second principle of color mixing of lights is this: any color at all can be made from three different colors, in our case, red, green, and blue lights. By suitably mixing the three together we can make anything at all, as we demonstrated with our two examples. Further, these laws are very interesting mathematically. For those who are interested in the mathematics of the thing, it turns out as follows. Suppose that we take our three colors, which were red, green, and blue, but label them A, B, and C, and call them our primary colors. Then any color could be made by certain amounts of these three: say an amount a of color A, an amount b of color B, and an amount c of color C makes X:

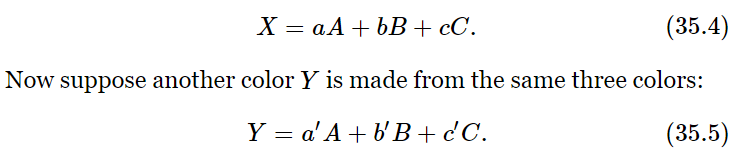
Then it turns out that the mixture of the two lights (it is one of the consequences of the laws that we have already mentioned) is obtained by taking the sum of the components of X and Y:

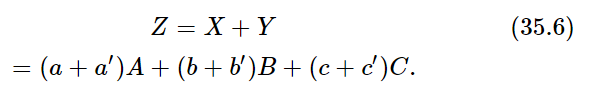
It is just like the mathematics of the addition of vectors, where (a,b,c) are the components of one vector, and (a′,b′,c′) are those of another vector, and the new light Z is then the “sum” of the vectors. This subject has always appealed to physicists and mathematicians. In fact, Schrödinger wrote a wonderful paper on color vision in which he developed this theory of vector analysis as applied to the mixing of colors. ¹

Now a question is, what are the correct primary colors to use? There is no such thing as “the” correct primary colors for the mixing of lights. There may be, for practical purposes, three paints that are more useful than others for getting a greater variety of mixed pigments, but we are not discussing that matter now. Any three differently colored lights whatsoever ² can always be mixed in the correct proportion to produce any color whatsoever. Can we demonstrate this fantastic fact? Instead of using red, green, and blue, let us use red, blue, and yellow in our projector. Can we use red, blue, and yellow to make, say, green?

By mixing these three colors in various proportions, we get quite an array of different colors, ranging over quite a spectrum. But as a matter of fact, after a lot of trial and error, we find that nothing ever looks like green. The question is, can we make green? The answer is yes. How? By projecting some red onto the green, then we can make a match with a certain mixture of yellow and blue! So, we have matched them, except that we had to cheat by putting the red on the other side. But since we have some mathematical sophistication, we can appreciate that what we really showed was not that X could always be made, say, of red, blue, and yellow, but by putting the red on the other side we found that red plus X could be made out of blue and yellow. Putting it on the other side of the equation, we can interpret that as a negative amount, so if we will allow that the coefficients in equations like (35.4) can be both positive and negative, and if we interpret negative amounts to mean that we have to add those to the other side, then any color can be matched by any three, and there is no such thing as “the” fundamental primaries.

We may ask whether there are three colors that come only with positive amounts for all mixings. The answer is no. Every set of three primaries requires negative amounts for some colors, and therefore there is no unique way to define a primary. In elementary books they are said to be red, green, and blue, but that is merely because with these a wider range of colors is available without minus signs for some of the combinations.

_________________________________________________________
Margin

1- Über das Verhältnis der Vierfarben- zur reifarbentheorie, Sitzungsberichte der Akademie der Wissenschaften in Wien. Mathematisch-naturwissenschaftliche Klasse, Abteilung 2a, 134, (1925), 471-490.

2- Except, of course, if one of the three can be matched by mixing the other two.

مواضيع ذات صلة

The sensation of color

Physiochemistry of color vision

The mechanism of color vision

The chromaticity diagram

Color depends on intensity

Aberration

The ω,k four-vector

Moving sources

Anomalous refraction

The intensity of reflected light

Optical activity

Polarizers