Schrödinger Equation
المؤلف:
Calogero, F. and Degasperis, A
المصدر:
Spectral Transform and Solitons: Tools to Solve and Investigate Nonlinear Evolution Equations.New York: North-Holland
الجزء والصفحة:
...
23-7-2018
2544
Schrödinger Equation
The Schrödinger equation describes the motion of particles in nonrelativistic quantum mechanics, and was first written down by Erwin Schrödinger. The time-dependent Schrödinger equation is given by
![ih(partialPsi(x,y,z,t))/(partialt)=[-(h^2)/(2m)del ^2+V(x)]Psi(x,y,z,t)=H^~Psi(x,y,z,t),](http://mathworld.wolfram.com/images/equations/SchroedingerEquation/NumberedEquation1.gif) |
(1)
|
where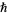 
is the reduced Planck constant 
, 
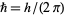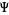is the time-dependent wavefunction, 
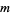is the mass of a particle, 
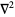is the Laplacian, 
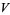is the potential, and 
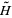is the Hamiltonian operator. The time-independent Schrödinger equation is
![[-(h^2)/(2m)del ^2+V(x)]psi(x,y,z)=Epsi(x,y,z),](http://mathworld.wolfram.com/images/equations/SchroedingerEquation/NumberedEquation2.gif) |
(2)
|
where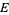 
is the energy of the particle.
The one-dimensional versions of these equations are then
![ih(partialPsi(x,t))/(partialt)=[-(h^2)/(2m)(partial^2)/(partialx^2)+V(x)]Psi(x,t)=H^~Psi(x,t),](http://mathworld.wolfram.com/images/equations/SchroedingerEquation/NumberedEquation3.gif) |
(3)
|
and
![[-(h^2)/(2m)(d^2)/(dx^2)+V(x)]psi(x)=Epsi(x).](http://mathworld.wolfram.com/images/equations/SchroedingerEquation/NumberedEquation4.gif) |
(4)
|
Variants of the one-dimensional Schrödinger equation have been considered in various contexts, including the following (where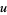 
is a suitably non-dimensionalized version of the wavefunction). The logarithmic Schrödinger equation is given by
 |
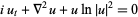(5)
|
(Cazenave 1983; Zwillinger 1997, p. 134), the nonlinear Schrödinger equation by
 |
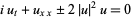(6)
|
(Calogero and Degasperis 1982, p. 56; Tabor 1989, p. 309; Zwillinger 1997, p. 134) or
 |
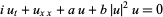(7)
|
(Infeld and Rowlands 2000, p. 126), and the derivative nonlinear Schrödinger equation by
 |
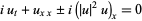(8)
|
(Calogero and Degasperis 1982, p. 56; Zwillinger 1997, p. 134).
REFERENCES:
Calogero, F. and Degasperis, A. Spectral Transform and Solitons: Tools to Solve and Investigate Nonlinear Evolution Equations.New York: North-Holland, p. 56, 1982.
Cazenave, T. "Stable Solution of the Logarithmic Schrödinger Equation." Nonlinear Anal. 7, 1127-1140, 1983.
Infeld, E. and Rowlands, G. Nonlinear Waves, Solitons, and Chaos, 2nd ed. Cambridge, England: Cambridge University Press, 2000.
Tabor, M. "The NLS Equation." §7.5.c in Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, p. 309, 1989.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, p. 134, 1997.
الاكثر قراءة في المعادلات التفاضلية الجزئية
اخر الاخبار
اخبار العتبة العباسية المقدسة
